232 (50)

METODY NUMERYCZNE... id/232

węzłowymi ze względu na ciągłe „sklejanie" wielomianów z poszczególnych elementów. Natomiast punkt Q⁽p na c_x może być wybrany dowolnie (wyżej Q- (i +0.5) A) tak aby tylko był różny od x, i jr_ł+1. Zmieniając położenie O*- - otrzymujemy różne funkcje bazowe w przestrzeni

(d) k — 3. W tym przypadku vz i)[^3> na elemencie e, ma być wielomianem trzeciego stopnia

i|„(x) = a^-Mi^+ai^+ai⁰

Do jego wyznaczenia należy podać cztery warunki (parametry). Mamy tutaj dwie możliwości: podać parametry Lagrange'owskie albo Hcrmite'owskie. W pierwszym przypadku wybieramy cztery węzły z e_x zawierające koniecznie punkty X: i x₍ +, ze w/glcdu na ciągłość funkcji v i zadajemy w nich wartości funkcji v (parametry węzłowe). Dalszy opis jest analogiczny do przedstawionego w (c) i dlatego pomijamy go. Dokładniej natomiast omówimy konstrukcję przestrzeni z parametrami Hernrite’owskimi.

W tym przypadku na węzły' z c, przyjmujemy punkty' = x_t i (jj^J = = x_i+_l, za parametry węzłowa zaś wartości i'(fij⁰) i Dv iQ^fV), j = l,2.Taki wybór zapewnia jednoznaczność wielomianów' na a, i ciągłość w [0, /] funkcji v wraz /. pierwszymi pochodnymi. Skonstruowana w ten sposób przestrzeń KJ³⁾ ma dodatkową własność, jest zawarta w H², cr H². Jeśli przyjąć, że funkcje v g T7³⁾ zerują sic w punktach brzegowych wraz z pierwszymi pochodnymi, to V£³⁾ cr H². Przestrzeń V^<3) może być wykorzystana do konstrukcji MES również dla równań różniczkowych czwartego rzędu z odpowiednimi warunkami brzegowymi. Takie zagadnienie rozpatrzymy dalej.

Określmy funkcje bazowe w przestrzeni Tym razem każdemu węzłowi Q\^iJ (QT ⁼⁼ £?^(Ii⁺¹⁾)> ^óry oznaczmy przez Q^ll\ odpowiadają dwie funkcje: fp^u} i i/⁰. Mają one spełniać następujące warunki (Q^ip) e e_p):

<p^(Q^ip]) = s_ip,    zy‘>₍Q<») = o

^\Q^) - 0

dla i = J,..., /u; p = 0,.... m+ 1 i dodatkowo jeszcze w przypadku funkcji )/'■' dla / = 0, i = 777+1. Rozszerzenie zakresu zmienności indeksu dla funkcji Tp^u) wynika stąd, źe nie znamy wartości pierwszej pochodnej rozwiązania w punktach

x = 0 i x = /.

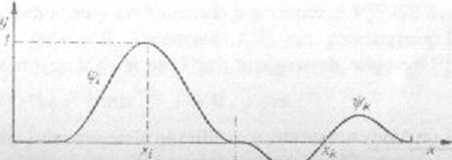
RYS. 10.11