23 (127)

42

1.4. ŻEGLUGA MIESZANA

Luk onodromy na skutek tego, że swoją wypukłością jest skierowany w stronę bliższego bieguna, powoduje, ze często droga po or todromie prowadzi przez radony lezące w dużych szerokościach geo graficznych, przez która ze względu na warunki lodowa, zł* pogodę czy też z innych przyczyn statek ma powinien przechodzić Mamy więc do czynienia z sytuacja, w której ze względu na ważne przyczyny statek ma powinien przekraczać równoleżnika określonej szerokości, zwanego równoleżnikiem ograniczającym ( f ).

W takich wypadkach stosuje się tzw. żeglugę mieszań*, przy której droga sutku jest najkrótsza w porównaniu z każdą inną. nie

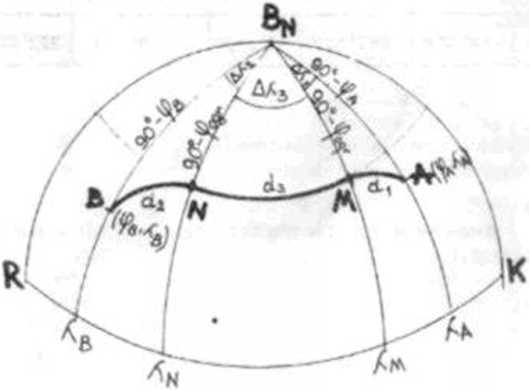
«v». 1.14. Żeewaa WMNM

przecinając* równoleżnika ograniczającego Droga statku w takim wy padku składa się z trzech odcinków (ryt.1.14):

- ortodromy AM - od pozycji wyjścia Ipkt Aj do równo leż nike ograniczającego (pkt. M).

-    loksodromy MN - pokrywając#) się z równoleżnikiem ograniczający m (od pkt M do pkt. N),

-    ortodromy NB od równoleżnika ograniczającego (pkt. N) do pozycji przybycia (pkt. B).

Z powyższych wyjaśnień wynika, że w celu rozwiązania próbie mu żeglugi mieszanej należy rozwiązać dwie ortodromy:

1. ORTODROMĘ AM. w której punkt A o współrzędnych geograficznych (|?_A, A_a jest punktem wyjściowym, a punkt Mo współrzędnych ©    • lP . A., punktem kodcowym. W punkcie M orto-

dr oma jest styczna do równoleżnika ograniczającego, tworząc z południkiem pozycji kąt prosty. Tak więc punkt M to jednocześnie wierzchołek ortodromy AM Współrzędne wierzchołka tej ortodromy wynoszą:

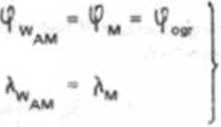
0.45)

2 ORTODROMY NB. w której punkt N o współrzędnych ge ograł icznych.    ^A_N jest punktem wyjściowym, a punkt

B o współrzędnych geograficznych    A_H punktem kodcowym.

Zatem punkt N to jednocześnie wierzchołek ortodromy NB o współ • rzędnych:

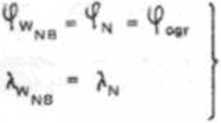
(1 461

Jeżeli znane są współrzędna punktów A i 8 oraz szerokość równoleżnika ograniczającego ( (p^ ), to możemy obliczyć drogą po