289

6.1. UKŁADY PODSTAWOWE WŁAŚCIWOŚCI I WIELKOŚCI ZALEŻNE 289

U_l-U₂ = UAl +

1

= U_t

(6.45)

A-l) ^{1 2 3 4 5}\A-l Po podstawieniu równania (6.45) do prawej strony równania (6.43), otrzymuje się

(6.46)

2(U₁-U₂)”^’sin(nn/A)    ,    ^

u =---— > -cos(na»_st)

"    n = 1    ⁿ

Z równania (6.46) wynika oczywisty wniosek, że w napięciu u pojawia się maksymalna wartość amplitudy składowej oscylacyjnej rzędu n = 1 przy A = 2. Ponieważ dla A = 2 jest U₂ = — U_l = (U ₂ — U J/2, więc u_{n = 1} = (4/n)U_t lub —(4/n)U₂.

Na rysunku 6.6b przedstawiono praktyczny układ przekształtnika z rys. 6.6a, przy założeniu, że U _t < U₂ i A < 2. W tym przypadku energia pobierana ze źródła napięciowego U _v (np. z ogniwa słonecznego) jest przekazywana poprzez dławik L do baterii U₂. Jeśli przyjąć A > 2, to ze źródła U₁ jest pobierany tylko prąd magnesujący dławika L.

W układach z rysunku 6.6 źródło prądowe / spełnia rolę „czerpaka” energii — pobiera energię ze źródła napięciowego U_t i przekazuje następnie do źródła napięciowego U₂. Analogiczną rolę może spełniać źródło napięciowe.

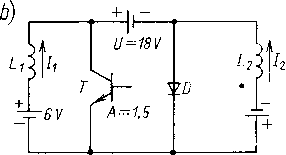
Na rysunku 6.7 przedstawiono układ przekształtnika z pośredniczącym źródłem napięciowym U, który jest dualny z układem z rys. 6.6a.

12 V

a)

u,

=i⁷.S₁

(6.47)

(6.48)

(6.49)

19 Eneraoelektronika

1

Rys. 6.7. Przekształtnik napięcia stałego na napięcie stałe z pośredniczącym źródłem napięciowym: a) układ podstawowy; b) przykład układu

Niech H j oznacza funkcję stanu łącznika S_1; a H₂ funkcję stanu łącznika S₂. Analogicznie jak w odniesieniu do układu z rys. 6.6a, otrzymuje się trzy wielkości zależne, określone następującymi równaniami:

u₁ — H_l ■ 0 + H₂U u₂ = -H₁U + H₂ 0

2

= H_lI₂ + H₂I_l

3

Dualność równań opisujących wielkości zależne układów z rysunków 6.6a

4

i 6.7a jest oczywista. Wychodząc z analogii tych równań, otrzymuje się zależność

5

(6.50)