293 [1024x768]

302

ROZTWORY I RÓWNOWAGI FAZOWE

Destylacja

Przeanalizujmy dokładniej prosty diagram wrzenia (rys. 4.12) dla układu doskonałego lub dla układu wykazującego niewielkie odstępstwo od doskonałości. Weźmy roztwór o początkowym składzie (a) i poddajmy ogrzewaniu. Po osiągnięciu temperatury T, ciecz zaczyna wrzeć, gdyż osiągnęliśmy krzywą równowagi ciecz—para. Skład pary (b) jest bogatszy w składnik A; może być łatwo odczytany na krzywej składu pary. Taki jednorazowy krok jest mało

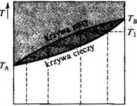
dc    ba

100* A    100*1}

Rys. 4.12. Prosty diagram procesu destylacji frakcyjnej

efektywny, jeżeli chodzi o wzbogacenie jednego ze składników, chyba że różnią się one bardzo znacznie temperaturą wrzenia. W praktyce stosuje się proces destylacji frakcyjnej, w której jednostkowy etap wzbogacenia przedstawiony poprzednio jest powtórzony wielokrotnie poprzez skroplenie wydzielającej się pary, kolejno odparowanie nowego roztworu, znów skroplenie i odparowanie itd. Procedura taka odpowiada przejściom schodkowym pokazanym na rys. 4.12.

Po przeprowadzeniu 3 kolejnych procesów odparowania i kondensacji pokazanych na rysunku uzyskujemy destylat o składzie d. Schodkowy proces destylacji odbywa się w praktyce automatycznie w kolumnach destylacyjnych, których budowę przedstawiono schematycznie na przykładzie urządzenia laboratoryjnego i przemysłowego (rys. 4.13, 4.14). W kolumnie przemysłowej możemy wyróżnić poszczególne półki, na których odbywają się kolejne etapy procesu schodkowego. Para wydzielająca się podczas wrzenia destylowanej cieczy przechodzi do pierwszej półki, tu się skrapla, powodując odparowywanie bardziej lotnej cieczy, bogatszej w składnik lotnicjszy. Para wydzielająca się z pierwszej półki kondensuje się na drugiej półce, skąd ulatnia się para jeszcze bogatsza w składnik lotnicjszy itd. Wzbogacanie na każdej półce jest oczywiście mniejsze od wzbogacenia teoretycznego równoważnego jednemu schodkowi na krzywej z rys. 4.12. Gdy wzbogacenie jest równoważne jednemu