277 [1024x768]

286

ROZTWORY I RÓWNOWAGI FAZOWE

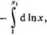
— Iń jc, =

A//. f dr r !r^ł

A H_w / 1

r \ r,

a//* / r-r, \ r \ r r, /

(4.29)

Jeżeli podwyższenie temperatury wrzenia jest niewielkie, iloczyn T• r, można zastąpić przez T\; x_x możemy z kolei zastąpić przez l-*₂, a dla bardzo małych wartości x₂ wyrażenie -ln(l-x₂) równe jest wprost x₂. Stąd

A//.

RT\

at_w

a więc otrzymujemy równanie identyczne z równaniem (4.22).

Podobnie prowadzone rozważania dla procesu krzepnięcia prowadzą do analogicznego wzoru na obniżenie temperatury krzepnięcia

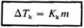
(4.30)

gdzie stała kriometryczna

(4.31)

RT\ M_x 1000 A//*

przy czym T_x jest temperaturą krzepnięcia czystego rozpuszczalnika, a A//_k — ciepłem topnienia 1 moła czystego rozpuszczalnika.

W tabelach 4.1 i 4.2 zestawiono dane'fizykochemiczne dla niektórych najważniejszych rozpuszczalników stosowanych w ebuliometrii i kriometrii.

Tabela 4.1

Stale ebuliometrycznc niektórych rozpuszczalników

Rozpuszczalnik	A//w(cal/mol)	Tt	/fw(deg- kg/mol) obliczone	A\«(deg • kg/moł) doświadcz.
Woda	9720.	373,16	0.514	0,51
Chloroform	7020	334.4	3,78	3.77
Alkohol etylowy	9220	351,7	1,227	1.20
Benzen	7350	353.3	2.642	2,63

Jak widzimy zgodność pomiędzy obliczonymi na podstawie wzorów (4.24) i (4.31) a znalezionymi doświadczalnie wartościami i K_k jest na ogół bardzo dobra.

Pomiary ebuliometryczne, a zwłaszcza kriometryczne są szeroko stosowane w badaniach fizykochemicznych. Najbardziej ogólnym zastosowaniem jest