2

Zmienna w szeregu czasowym jest często oznaczana przez Z_t w celu odróżnienia od zmiennych X i Y stosowanych w analizie regresji i innych dziedzinach. Konkretną wartość zmiennej w czasie t (obserwację) oznaczamy przez z_r Odchylenie występujące w czasie t oznaczamy przez a_r Odchylenie a, w modelu szeregu czasowego służy takim samym celom, jak składnik losowy regresji e. Zakładamy, że a, (odchylenie losowe w czasie t) ma zerową wartość średnią i stałą wariancję er² oraz że kolejne odchylenia nie są wzajemnie skorelowane.

Przy zastosowaniu takiego zapisu do szeregów czasowych modelem procesu błądzenia przypadkowego jest równanie (12.1).

Proces błądzenia przypadkowego:
Z( —Z(_i = at
lub równoważnie:	(12.1)
Z, = Zt_x + at.

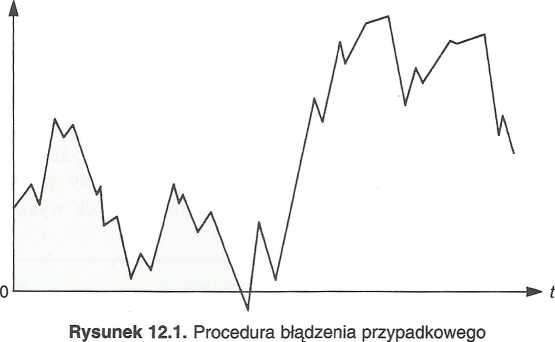
Równanie (12.1) mówi, że różnica między wartością zmiennej Z w czasie t i jej wartością w czasie t-1 jest odchyleniem losowym. Szereg czasowy Z_t jest szeregiem błądzenia przypadkowego, jeśli każdy krok od t- 1 do t jest po prostu losowym odchyleniem a_t. Przykład procesu błądzenia przypadkowego przedstawiono na rysunku 12.1. Jak widać, ruchy zmiennej Z, w czasie nie odbywają się ani według żadnych schematów, ani według trwałego trendu. Różnica między ceną akcji jutro a ceną akcji dzisiaj jest zupełnie losowym „odchyleniem”. Ponieważ odchylenia a_t nie można prognozować, jako że jest zupełnie losowe, nie możemy również prognozować Z₍. Najlepsza możliwa w tym przypadku prognoza przewidująca dla odchylenia a_t wartość równą jego wartości średniej, czyli zero,

Z,

622