2 (456)

62

III. Teoria błędów

3. Prawdopodobieństwo P^ jednoczesnego wystąpienia szeregu błędów ^e-i> s_?,s_n w przedziałach od e_t do s_t+ds wynosi

P =    ~^ri.4)

Aby okręcić przebieg funkcji prawdopodobieństwa (HL1)_Ł czyli wyznaczyć parametr k, posłużono się postulatem-o-średniej arytmetycznej^ który wymaga, aby prawdopodobieństwo P jednoczesnego wystąpienia³ szeregu błędów osiągnęło wartość maksymalną.

— JKalezy Więc znaleźć maksimum wyrażenia (1II.4), tzn.---    _

i— ___Jiⁿe~^h2^ -== maksimum.    ~

Obliczająć pochodną względem A i przyrównując ją do zera^etrzy-mamy równanie określające A:    —:

a(h*e ^hM) i_w^i_e-AV]^V^=2L2lee](-2A[s^), dih

_hn~l    ^ _ _2fe2 [_ee]) |0,

Jl² =

n

2[ee]

2 [es],

Oznaczając [sejfu przez m\ (jako kwadrat średniego błędu spostrzeżenia), mamy h* = l/2m*, czyli ^r

I    (rii.5)

m₀Y 2

Po podstawieniu tej wartości do wzoru (III.1), otrzymamy nową postać równania funkcji prawdopodobieństwa f{s), którą nazywamy rozkładem normalnym Gaussa:

/(«) =    exp j

B

(III. 6)

m₀ /2tz

Przekształcając (HI.5), otrzymamy wzór na średni błąd spostrzeżenia m₀, wyrażony przez parametr h:

m₀ =

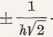
(in.7>

Ponieważ wzór ten określa także wartość błędu e w punkcie przegięcia, wypływa więc stąd ważny wniosek:

Średni błąd spostrzeżenia m₀ róumy jest rządnej w punkcie przegięcia krzywej prawdopodobieństwa.

2. Obliczanie prawdopodobieństwa występowania błędów. Obliczanie prawdopodobieństwa występowania błędów na podstawie równania (m.2) jest w praktyce kłopotliwe i dlatego funkcję pod całką rozwija się w szereg Maclaurina.