30skladanie drgan harmonicznych

SKŁADANIE DRGAŃ HARMONICZNYCH Ruchy harmoniczne są często ruchami złożonymi z kilku lub nawet znacznej liczby ruchów harmonicznych. Ograniczymy się do analizy złożeń dwóch drgań.

Składanie drgań równoległych Mamy dwa drgania składowe:

x_t = A, cos(coj + <5,) = A, cos <p, x₂ = Ą cos (co₂t + d₂) = A₂ cos tp₂

Założymy, że Ą > 0 i A₂ > 0. Jeśli tak nie jest to znak (-) można uwzględnić w fazach <5, i ć)₂,np. -Acos(cot + 5) = Acos(cot +3 +n).

Drganie wypadkowe dane jest równaniem

x(l) = .v,(/) + x-,(t) = Ą cos<p, + A₂ cos<p₂ = yJ(/)cos[9(/)]

Złożenie dwóch drgań równoległych o dowolnych amplitudach można analizować używając metody wektorowej lub metody wskazów.

Diagram wektorowy

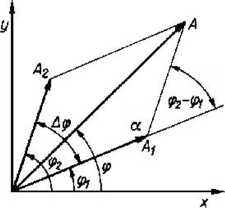
Z twierdzenia kosinusów

A = Ą + A; - 2 A, A₂ cos a = -Ja? + A₂ + 2 A, A₂ cos(<p₂ -ę_t)

A, sinip, + ^,sino),

tg<P = T---f-~

A_x cos<p, + A₂ cos<p₂

'Lx = Ą + Ą> A*_m=\A~^Ai\

Jeśli <p, i/lub <p₂ są funkcjami czasu to zarówno amplituda A jak i faza tp są funkcjami czasu. Występuje modulacja amplitudy i fazy (bądź częstości).

Dodawanie drgań prostopadłych

Weźmy pod uwagę drganie punktu materialnego będące wynikiem nałożenia się dwóch drgań harmonicznych odpowiednio wzdłuż osi x i y. x = A_x cos(gj_j t + tp_x) I

> - równanie toru w postaci parametrycznej y = A_ycos((o_yt + ę_y)\

Położenie punktu może być opisane wektorem r(t) = x(t)e_x +y(t)e_v Niektóre szczególne przypadki, gdy (»_x = co_y = (O, (p_x = 0, (p. = Aę x = A_x cos {(Ot) y = A_v cos(cot + Aę)

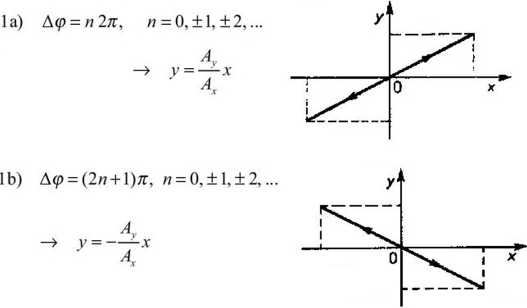
2a)

A<p = (2n +,

n = 0, ± 1, +2,...

Ą = A_y = A

x +y

równanie okręgu

2b) Aę» = (2w + l)j,

n = 0, +1, ±2,...

A_x * A_y

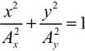
równanie elipsy

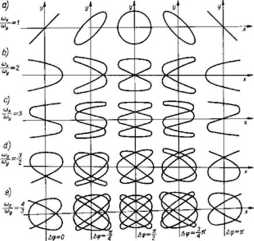
Przypadek ogólny: krzywe Lissajous