35 (321)

68

słupami AC. Drugie końce belek spoczywaj? swobodnie na podłodze,na-tomiast drugie końce słupów są zamurowane. Punkty 0, w których zbić nik opiera się o belki leżę w połowie długości tych belek.

Zakładajęc gładkość wszystkich powierzchni oraz symetrię układu względem płaszczyzny zy (rys. I.56a) określić:

-    nacisk zbiornika na ścianę,

-    nacisk końców belek na podłogę,

-    raakcje w zamurowaniu C.

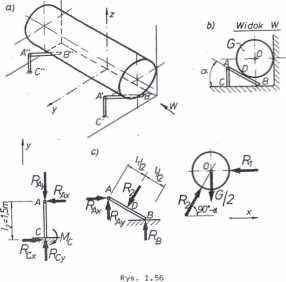
Rozwlęzanie

W przypadku symetrii układu względem osi yz zadanie można sprowadzić do dwóch identycznych, płaskich układów sił działajęcych w płaszczyznach belki i słupa. Siłę zewnętrznę dla pojedynczego układu sił będzie połowa siły ciężkości zbiornika -5- (całkowity ciężar zbiornika rozłoży się równo na dwie siły działajęce w obu płaezczyz nach: C'A'B'oraz C"A”B").

Aby rozwiązać zadanie trzeba rozpatrzyć kolejno, uwolnione od więzów: zbiornik, belkę AB i słupek AC (rys. I.56c). Na uwolniony od więzów zbiornik (a właściwie Jego połowę) działaję więc: połowa siły ciężkości zbiornika oraz reakcje od ściany Rj i od balki Rg-Obie reakcje przy pominięciu tarcia sę prostopadłe odpowiednio do powierzchni ściany oraz osi belki. Kierunki działania tych sił (rys. 1.56c) , zgodnie z twierdzeniem o trzech siłach, muszę przecinać się w Jednym punkcie O, co wynika również stęd, że siły Rj 1 R_£ muszę być normalne do powierzchni walca (pomijamy tarcie). Z warunków równowagi (z sumy rzutów sił na osie x i y) wynika, że

^R1 ■■§■ *9* ■ 5773,5 N.

Sumaryczny nacisk zbiornika na śclonę będzie równy, co do wartości, dwóm siłom Rj (jedna działajęca w płaszczyźnie C'a'b',druga w płaszczyźnie C-A"B~). tak więc

11 547 N.

Rozpatrzmy teraz równowagę jednej z belek uwolnionej od więzów. W przegubie A występuje reakcja posiadajęca składowę poziomę R_Ax i pionowę R_Ay, natomiast w punkcie B reakcja podłogi jest skierowana pionowo w górę, gdy pomijamy tarcie (wszystkie powierzchnie elementów sę z założenia gładkie). Równania równowagi belki

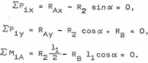
Po rozwięzaniu tego ukł*du równań otrzymujemy

6667