35 (554)

Biblioteczka Opracowań Matematycznych

£(-)= \fMf_y{z-x)dx = \f_y{z-x)dx

Dla z < O, z - x < O stąd g(ź) = 0.

Dla z > 2, z - x > 1 stąd g(z) = 0.

Dla O < z <2:

Funkcja podcałkowa będzie różna od zera tylko dla x, które spełniają warunek: 0 <z -x < 1 co po przekształceniu daje: z-l <x < z.

Mogą wystąpić dwa przypadki:

I: 0 <z < 1 wówczas: sO = \f_y{z -x)dx = \dx = [x l = 2

o    o

II: l<z<2 wówczas: g(z)= )f_y{z-x)dx = \dx = [xl,=2-z

__    Z-\ _m    2-1

Ostatecznie gęstość Z = X + Y można zapisać:

0 dla z < 0; z > 2;

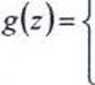
z dla 0 < z < 1 2 - z dla I < z < 2

92/ Niezależne zmienne losowe X i Y mają rozkłady:

dla y€<0,l> dla y&<0,1 >

Ae

dla *>0; ż>0 0 dla *<0.

Znaleźć rozkład zmiennej losowe Z = X + Y. Rozwiązanie:    «

Podobnie jak w przykładzie 91/ :#(z) = j/_r(x)/|.(r-x)c& Dla z <0 tzn. x + y <0 jest g(z) = 0.

Dla z >0 rozpatrujemy dwa przypadki:

0 < z <] czyli 0< z - x < 1

/,(*)=

fy{y) =

-CC

/K²) =    fAe * ldx = [-e^J-*l = l-e^

-cc    0

II: z >1; 0 < z-x < 1 czyli z-l<x<z

g(*)= Jte^cbcĄ-e    =e-^Js(e‘ -l)

2-1

93/ Wiedząc, że gęstość dwuwymiarowej zmiennej losowej wyraża się wzorem:

e ⁽'^ł>) dla x,y > O O poza

f(x,y)=

Znaleźć EZ oraz D² Z dla Z = 2X + Y.

Rozwiązanie:

Konieczne jest wyznaczenie gęstości brzegowych dla zmiennych X oraz Y.

= e

/,(*)= \f{x,y)dy =    f e⁽**^y)dy    = lim \e~^l‘*^y)dy    = lim [-    e“^(jrł>)J, = limf    -^ + 4

•    ^J    k -* x J    k -*<c    k-¥<x>\    o''    ' a

x    O    O    \ ^c    c /

Podobnie obliczając gęstość brzegową f_y(y) otrzymujemy:

f>{y)=\^eĄ“^{y)dx =} e-^y

o

Obliczając EZ oraz D²Z skorzystamy z własności wartości przeciętnej i wariancji.

EZ = E(2X + Y) = 2EX + EY

ac

EX = \xe~^xdx = 1im[-jte ^x -e = lim(-ke~^k-e~^k + 0 + l)=l

Powyższą całkę obliczono metodą przez części. Pomocniczo także wyznaczono granicę:

lim (- ke ^K )= f- oo 0l= lim —

-k

00

00

lim

k-*x

= 0

Podobnie obliczymy, że jye ^}dy-1 A zatem: EZ = 2EX + EY = 3°

Do wyznaczenia wariancji obliczamy pomocniczo: E(X²) oraz E(Y²).

e(.Y²)= jx²e-^xdx=\m[-x²e ‘-2xe ¹ - 2e ' J =2 0

Całkę obliczono metodą przez części.

Podobnie E(Y²) = 2.

A zatem:

D² X = E(X²) - (EX)² = 2 - 1 = 1 D²Y = E(Y²) - (EY)² =2-1 = 1

D² Z = D² (2X +Y) = D² (2X) +D²Y= 4D² X+D²Y = 4+1=5 94/ Dwuwymiarowa zmienna losowa Z =(X, Y) ma gęstość postaci: l

md'

dla x²+y²<a‘ 0 dla x² + v² > a

/(+>•)=•

-69-