08 (4)

46/

Biblioteczka Opracowań Matematycznych

x³ + io = t*

Jx^J Vx’ + I0dx = 3x'dx = 2idl

2 dl

x^:dx =

= - frdt = -V + C i J o

²V(*^;+io y,,

.tir

47/ f _

^J x⁴ + 1

x = l 2 xdx - dt

xdx = ^d-L 2

¹    ,,    1    j    _

= —arctet + c = —arctgx + C + 12 2

^ Jsin³ xć/x= Jsin²xsinxćZv= J(l -cos² x)sinx<iv= jsinxah- Jcos² xs\nxdx=

=-cosc-

cosK=t sircc dx=di

«    /²    co^ X

=-cosr+ k^:ć/r=-coa:H—tC=-cosc-t--hC

J    i

49/

r 5x²dv

x³ =/

<*

vl-x⁶

3x²cZr = c/rl = 5 f . ^    = - f ^ =-arcsin/+C = -arcsinx³+C

2 , dt x dx = — 3

Całkowanie przez podstawienie to jedna z najważniejszych metod całkowania. Stosujemy ją wówczas gdy zastosowanie nowej zmiennej dla fragmentu wyrażenia podcałkowego upraszcza całkę. Nie ma niestety ogólnych przepisów kiedy i jak tego dokonać. Umiejętność doboru odpowiedniego podstaw ienia nabywa się drogą wprawy. Z całą pewnością metodę tą możemy zastosować gdy licznik ułamka podcałkowego jest pochodną mianownika. Korzystamy wówczas ze wzoru:

(1.22)

rf'(x)dx

^J f(x) 3. Całkow anie przez części

Całkowanie przez części stosuje się wówczas, gdy pod całką występuje iloczyn funkcji algebraicznej lub przestępnej. Całkowanie przez części odbywa się według wzoru:

(1.23)

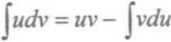
przy czym jako funkcję w, przyjmuje się funkcję, której różniczkowanie upraszcza wyrażenie podcałkowe, a za dv tę część wyrażenia podcałkowego, którego całka jest znana lub może być łatwo wyznaczona.

PRZYKŁADY CAŁKOWANIA

jxsin xdx =

= -xcos x + sin x + C

u = x    du = dx

dv = sin xdx v = - cos x

= -x cos x +

Jcos xdx =

J x² cos xdx =

u = X¹    du - 2xdx

dv = cos xdx v = sin x

li

= X¹ sin x + 2x cos x - 2 sin x + C

(Dla obliczenia całki (51) wykorzystano całką (50)).

52/

= x² sin x - 2 J .v sin xdx =

u = x du = dx dv = e¹ dx v = e¹

J xe ' dx =

JxV<fe =

¹ - je ^Xdx = xe ' - e' + C = x⁾e^t -3 jx²e^xdx =

- 3{x²e^x - 2 jxe ^xdx ) =

.    r    y    , I u = x du = dx

= x’e*-3x²e‘ + 6{xe^xdx =xⁱe^x-3x¹e^t + 6\    , =

•»    |rfv = e dx v = e

= x V - 3x V + 6xe^x - 6 je‘dx = x V - 3x^Je' + 6xe ’ - 6e^x + C

53/

= xV - 3

u = X¹ du = 3 x²dx dv = e‘dx v = e'

u = x'

ć/u = 2xd!x

= xV

- 15-