384 (6)

Etap wstępny (przyjmujemy „v° = 0)

,v^ 4- yj = ,v° + dx		T		r.o ob i		I
X^>2^> 4- V2 = X^() + ć/y	skąd : A =	i	, L =	-^r ~-p x°-xf		■"* ł - 2
4" ~ ‘3 ^=		i		r° - v~^>hX ~x3		— 3
.xf + vM=x»^.		i		l.v°-4\		-14_

P			|			'0.25
	p.					0.25
	p		1 w"'			0.25 0-25.
-	p_
			m~ _
y.Y	-d.V — “(A^7		PA)”^1 A^7 PL = 5.0			(x = x° +dx =5.0)
				-	4.0
			V = Ad y + L —		3.0
				2.0
				-9.0

	" 3 -1	-1	~i~		i m: ^vi
A(A^rPA)”^,A^7 =	-1 3	-1	-1		m: cov V'2
	-I -1	3	-1		cov
	... i _ i	-1	3		mi' ^•i _

'V(»io=i)

Przyjmijmy, że y= 0.95, skąd k~ 2. Przedział dopuszczalny _Av ma zatem postać Ay    - <-2; 2). Po obliczeniu wartości standaryzowanych esty

matorów poprawek

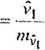
—= 2.31 £ Ay V3

i?2

v->    3

-----=-p-= 1.73 6 Av

^mv2 v3

*

^v3 - ~ ^u-

y^

= 1.15 e Ay

^v4

ffl;

V'4

yj

-5.19 t$Av

stwierdzamy, że 2 spośród nich (?], v₄) nie należą do przedziału, dla nich dopuszczalnego. Klasyczne' wyrównanie metodą t\'K stanowi więc tutaj jedynie krok „0” (krok startowy) w procesie iteracyjnego rozwiązania odpornego zadania wyrównawczego. W funkcji tłumienia Harnpela, oprócz k, jest konieczna jeszcze wartość k_fy Przyjmując k_h = 6 oraz V⁽⁰⁾ = V, P⁽⁰⁾ - P, obliczamy:

- wartości funkcji tłumienia

i-.(O) - s |Vj = v,j	6 ik\kb)	-> f(v,^(0)) =	b(0)l l I ^1 i......^k±
			k ~kb
(Ą^0) = £,)	€	li o t	1
=5,)	C- Av	-> «ff)=	1
i--(0) ! y: = v i	<= {k;kb)	-> -(vT>)=	N°’K
I 4 ‘M			* h

- macierz tłumienia

'/(v,^(0>)	0		0.92
			1
0	«5j^0)>			!
				0.20_

krok 1.

0.230

p(0 — ^rp(yó)))p(0) _

0.250

0.250

0.050

d⁽vⁿ = -(A^rP⁽¹⁾A)A^/-P⁽¹⁾L = 2.80

V^(l) =Ad⁽^ + L =

l .80^1		3.066 cov
0.80	c^(»	2.718
-0.20	• ^V(w0=l) "	2.718
-11.22		. cov 18.599

--(!} 1.80    . _/V5 ._

^vi ⁼ t—— = 1-03 e Av

¹    V3.06 6

3S5