416 (5)

Ustalenie macierzy kowariancji z uwzględnieniem błędności wektora X°

Traktowanie wektora X° jako zmiennej losowej o macierzy kowariancji C_xo =<⁷o.yQ_xo = <7oy*\\'^! wymaga ustalenia, odpowiadającej tej sytuacji, nowej macierzy kowariancji wektora wyrazów wolnych. Zauważmy bowiem, że skoro

L = x° - x^ob - F(X°) - x"^

gdzie losowym wektorem jest nie tylko x°^ó, lecz także X°, to przy założeniu wzajemnej niezależności tych zmiennych, należy zapisać

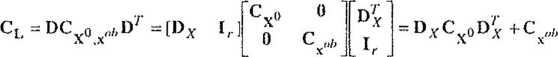
gdzie

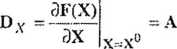
Zatem w ogólnym przypadku macierz kowariancji wektora wyrazów wolnych raa postać

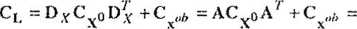
= (Jq_X AP_x A ^r + Oo P“^l

Wobec tego (dla d __v = -A^ L - OL, I) - -A^,

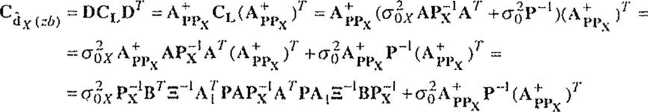
Ponieważ

A[PA = A / P[A, A₂ j = [A| PAj a[pA₂]=B

więc

C_a =(75_xPx^lB⁷'H-^|BP_x^lB⁷'““¹BP^ +a

C, =<r2_rP_x'B^r

^d.Y<rń) ^ox x

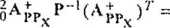
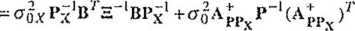
(9.27)

Biorąc pod uwagę, że _(W|) -(ToA^P ‘(A^/ oraz C_xo = <r$._v P£', macierz kowariancji estymatora przyrostów z uwzględnieniem macierzy kowariancji wektora X° można także przedstawić w postaci

= C oBY^P^+C

dv{bb)

(9.28)

Także w ustalaniu postaci macierzy kowariancji estymatora X-X°+dy należy uwzględnić, występujące tutaj, dwie wzajemnie niezależne zmienne

losowe: X°, d y - Estymator przyrostów d y, przez wyrazy wolne h - F(X°) -- x^ol>, jest jednak funkcją wektora X°, tzn.

=-a;; l =

Biorąc tę zależność pod uwagę, estymator

p_Pxlł-(X°)-^l

X = X^IJ -r d y przedstawimy w postaci

(9.29)

X - X° + d y = X° - App_x L = X° - a;_Px [F(X°) - x^ol> j = ~ ^X° ” ^APl»_xF(X⁰)+ Ap_Px x^ob

Stosując do wyrażenia (9.29) zasadę propagacji macierzy kowariancji oraz pamiętając, że X°, x⁰⁰ są wzajemnie niezależne, uzyskujemy

^x<r/>)    ^APP_x^A)Cx⁰^^{r A}pp_x ^A^ ^{+ A}pp_x*V^,a(^App_x

-    M)_} + A j_>Px C_x„i, (A _r»p_x )⁷ =

gdzie

M H - Ir ~ A;_Px A = I_r - Py¹¹ B⁷ »¹ A[PA

Et

= I_r-Px'lJ⁷’(BI^>x^,B^rr^lIi

(tutaj także A=—■    ). Macierz wykazuje własność (zob. rozdz. 5.2)

dX |x=x°

^MoPx^MS =^px Mg- Wobec tego

417