67 (92)

3.2.7. Układy równań, z których co najmniej jedno jest równaniem kwadratowym (I)

Rozpatrzmy układ dwóch równań o dwóch niewiadomych x i y, z których co najmniej jedno równanie jest równaniem kwadratowym. Oto przykłady:

Przykład układu równań o dwóch niewiadomych złożonego z równania liniowego i równania kwadratowego:

)mx + n = p - równanie liniowe z 2 niewiadomymi y * ar + bx + c - równanie kwadratowe z 2 niewiadomymi ( a / 0 )

Metoda algebraiczna polega na obliczeniu pary (par) liczb (*;y) spełniającej (spełniających) powyższy układ. W tym celu z równania liniowego obliczamy x lub y i podstawiamy do równania kwadratowego. Eliminując w ten sposób jedną niewiadomą, otrzymujemy równanie kwadratowe z jedną niewiadomą:

y = ~^x+-~\n^O -•7P ,v + -jj- = ax² + bx + c

Rozwiązując równanie kwadratowe ax²+ pi + ||| x + c - — = 0, wyznaczamy x, a następnie

y =-■7f .v + jf. Rozwiązaniem tego układu jest wyznaczona para liczb ( x; y) spełniająca dany układ równań.

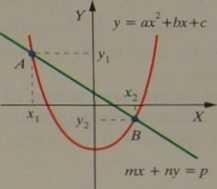
Metoda graficzna polega na narysowaniu w jednym układzie współrzędnych wykresów obu równań (paraboli i prostej z tego przykładu) oraz odczytaniu współrzędnych istniejących punktów wspólnych obu wykresów (np. paraboli i prostej: A (,v,; y,) i B ( x₂; y,)). Geometryczną interpretacją rozwiązania układów równań są istniejące punkty wspólne obu wykresów.

Uwaga: W przypadku, gdy w układzie dwóch równań jedno równanie jest stopnia pierwszego, to przedstawia ono prostą, a równanie drugiego stopnia - krzywą stopnia drugiego, na przykład parabolę, hiperbolę czy okrąg.

Zatem w rozwiązywaniu takiego układu chodzi o wzajemne położenie prostej względem krzywej drugiego stopnia. Stąd też układ może nie mieć rozwiązań, albo mieć jedno lub dwa rozwiązania. Oto przykłady:

Lliczba rozwiązań układu Przyklady'''^-\^	Brak rozwiązań		Rozwiązanie istnieje
			Jedno rozwiązanie		Dwa rozwiązania
prosta parabola ----	i	W		Y / '•yS(Xo-yo)		Y
	0	/ X		X	Yó	/ / ^x
prosta hiperbola ------	i	1	\ y		|	ta,;*)
	■	N	■	X	■
prosta okrąg	N r	y V	\ r	Y		Y
					l 0	x