Układy równań liniowych1

92 Układy równań liniowych

92 Układy równań liniowych

det -4

Liczbę x obliczamy ze wzoru x =

det /I =

1	1	0	0	1
0	T	1	0	0
0	0	1	1	0
0	0	0	1	1
10	0	0	0	1

det A

1	1	0	0		0	1	0	0
0	1	1	0		d)	1	1	0
0	0	1	1		0	0	1	1
0	0	0	1		10	0	0	1

= 1+10

1 1 0 1

0 0 0 1

= 11,

3 1 0 0 0 5 110 0 7 0 110 9 0 0 1 1 15 0 0 0 1

	110 0		5 1 0 0
	0 110		7 110
= 3	0 0 11		9 0 11
	0 0 0 1		15 0 0 1

detali =

Stąd x =    = 1.

Przykład 4.4

Rozwiązać podane układy równań metodą macierzy odwrotnej:

, _    „    ( x - 2y + 3z = -7

x + 7y = 2 .    ¹

2x - y = 9 '    ’

a)

3x + y + 4z = 2x + 5 y + z —

18

	1 1 0		7 1 0
= 3-5	0 1 1	+	9 1 1
	0 0 1		15 0 1

= -2 + 13= 11.

Rozwiązanie

Rozwiązanie X układu Cramera postaci AX = B będziemy wyznaczać ze wzoru

X = A~^lB.

a) Zapisując układ równań w postaci macierzowej otrzymamy

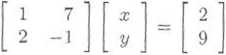
Zatem

13    1

czyli x = y, y =

b) Podobnie jak w poprzednim przykładzie mnożymy lewostronnie układ równań w P^0_ staci macierzowej przez macierz odwrotną do macierzy układu. Otrzymamy wtedy

X		‘ 1 -2	3 '
y	=	3 1	4
z		2 5	1
yli x	= 2,y = 3,z =		-1.

	' -7 ‘	1
	ó	~ 10
	18 .

-19

5

13

17

-5

-9

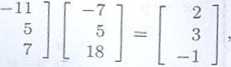
Rząd macierzy. Twierdzenie Kroneckera-Capellego

• Przykład 4.5

Znaleźć rzędy podanych macierzy wskazując niezerowe minory maksymalnych stopni

					" 1	0	1	0	3
■5	1	2	3 ‘		0	0	0	0	0
1	4	-1	2	; b)	2	0	1	0	1
9	-2	5	4		0	0	0	0	0
					3	0	1	0	-1

Rozwiązanie

Rzędem macierzy nazywamy największy stopień niezerowego minora tej macierzy, czyli wyznacznika utworzonego z elementów położonych w wybranych wierszach i kolumnach tej macierzy.

a) Dana macierz ma wymiar 3x4, a więc jej rząd może być równy 0,1, 2 lub 3. Wartości 0 i 1 można od razu wykluczyć, gdyż łatwo wskazać niezerowy minor stopnia 2, np.

5 1 1 4

minor

= 19 5^ 0 leżący w lewym górnym rogu macierzy. Należy teraz poszukać

niezerowego minora stopnia 3. Obliczamy wszystkie możliwe minory stopnia 3. Mamy

5 1 2		5 1 3		5 2 3		1 2 3
1 4 -1 9 -2 5	= 0,	1 4 2 9-2 4	= 0,	1 -1 2 9 5 4	= 0,	4-12 -2 5 4

Stąd wynika, że nie istnieje niezerowy minor stopnia 3, więc rząd danej macierzy jest równy 2.

b) Wszystkie minory danej macierzy zawierające parzyste wiersze lub parzyste kolumny są zerami. Minorem najwyższego stopnia nie zawierającym tych wierszy ani kolumn jest minor

1    1    3

2    1 1 3 1 -1

= 0.

Stąd wynika, że rząd danej macierzy jest mniejszy od 3. Wśród minorów stopnia 2 istnieje

minor niezerowy, np.

1 1 2 1

= -1 ± 0. Rząd danej macierzy jest więc równy 2.

•Przykład 4.6

Wykonując operacje elementarne na wierszach lub kolumnach podanych macierzy obliczyć ich rzędy:

0 CO 1 -		'234567'
4 5 7	; b)	8 7 6 5 4 3
1 -1 4		12 13 14 15 16 17
2 4 2		.18 17 16 15 14 13

Rozwiązanie

Wykorzystamy twierdzenie mówiące, że bez zmiany rzędu macierzy można w niej zamieniać wiersze (kolumny), mnożyć ustalony wiersz (kolumnę) przez stalą różną od zera oraz