1636661165

6-5

Układy równań. Równania wyższych rzędów.

Twierdzenie 6.8. Załóżmy, że f spełnia na każdym prostopadłościanie P C D warunek Lipschitza względem x. Wówczas dla każdego to £ R i każdego x₀ £ D istnieje dokładnie jedno nieprzedłużalne rozwiązanie zagadnienia początkowego

x' = f(x) x(to) = xo.

Niech cp: I —» Rⁿ będzie rozwiązaniem autonomicznego układu równań różniczkowych (UAn). Obraz {cp(t) : t £ 1} nazywamy krzywą fazową układu (UAn).

Rozważmy teraz autonomiczny układ dwóch równań różniczkowych

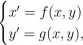
(UA2)

gdzie /, g: D —» R są funkcjami ciągłymi. Wykonując parę (formalnych) operacji możemy przekształcić układ (UA2) do postaci

(6.1)

g(x, y) dx - /(ar, y) dy = 0.

Załóżmy, że dla każdego (x,y) £ D zachodzi \f(x,y)\ + \g{x,y)\ > 0. Wówczas każdy punkt obszaru D jest punktem regularnym dla równania (6.1).

Niech 7 =    : I —* D będzie rozwiązaniem układu (UA2). Wtedy

krzywa regularna 7 klasy C¹ jest rozwiązaniem równania (6.1) w postaci parametrycznej.

Niech <h: D —> R będzie całką równania (6.1). Wówczas każda krzywa fazowa układu (UA2) jest zawarta w poziomicy całki $.

Jeśli dla każdej wartości C należącej do obrazu całki równanie

$(*,!/) = C

ma dokładnie jedno rozwiązanie y = r/(x] C), z pierwszego równania układu otrzymujemy rodzinę równań różniczkowych (sparametryzowanych stałą C)

x' = f(x,r/(x;C)).

Niekiedy można otrzymać „rozwiązanie ogólne” powyższej rodziny równań: x(t) =