36759 skan0339

342 Rozwiązywanie równań wyższych rzędów

W komórce A4 wpisujemy 1 (z = 1). W komórce B4 jako punkt startowy wybrano*] = 0,1. Do komórki B5 wprowadzono formułę

=$A$2*(B4+2*$D$2)/(B4*B4/$C$2+B4+$D$2)+$B$2/B4

i jako *2 otrzymano wartość 3,601 • 10^-2.

W tym miejscu należy zdecydować o formacie tej liczby. Wynik końcowy ma być określony z dokładnością do 3 cyfr znaczących, natomiast obliczenia prowadzi się zawsze z dokładnością o rząd większą, tak długo, aby ostatnia cyfra nie ulegała zmianie. Oznacza to, że wartość e nie może przekroczyć 5 • 10^-6.

W komórce C5 wpisano =B5-B4, co pozwala kontrolować przebieg obliczeń, np. czy proces jest zbieżny. W komórce A5 wpisano =A4+1 (liczba kroków). Po zaznaczeniu komórek A5: C5 „ciągniemy” uchwyt C5 w dół (czyli kopiujemy formuły obliczeniowe) tak długo, aż wartość bezwzględna liczby w kolumnie C będzie mniejsza od 5 • 10^-6. Jak widać, zostało to osiągnięte dla / = 15, a wynik końcowy wynosi 5,20 • 10^-2 ([PT] = 5,20 • 10~² M).

3. Rozwiązywanie uktadu równań nieliniowych

Jako przykład może posłużyć obliczenie rozpuszczalności Ca(OH)₂ w wodzie w 25°C, jeżeli znany jest jego iloczyn rozpuszczalności w tej temperaturze K_s = 7,9 ■ 10~⁶. Podobny problem występował w przykładzie 6.14. Wyprowadzono tam wyrażenie na rozpuszczalność:

c =

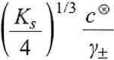
Do obliczenia średniego współczynnika aktywności y± wykorzystamy prawo Debye’a-Huckla (6.39) w postaci

lg y_± = -A

z+z-i g

\+4i ’

gdzie stała A w 298 K wynosi 0,5091 [M^_1/2], a siła jonowa roztworu, zgodnie z (6.17), jest równa /= 3c. Wyniki obliczeń w arkuszu kalkulacyjnym pokazano na rys. Dl.4.

W pierwszym przybliżeniu (i =1), obliczamy rozpuszczalność (C]), zakładając, że y± = 1 i tę wartość wpisujemy do komórki D3, a do komórki E3 wprowadzamy formułę =($D$1/4)^A(1/3)*1/D3. Wynik końcowy może być określony z dokładnością do 2 cyfr, toteż format w kolumnie E ustalamy na 3 miejsca znaczące (e < 5 ■ 10“⁵). Do pozostałych kolumn wpisujemy formuły zgodnie z tab. Dl.3.