1636661163

6-3

Układy równań. Równania wyższych rzędów.

Twierdzenie 6.3 (Twierdzenie Peano). Niech f: [to — 6, to + ń] x P —» Rⁿ będzie ciągłą funkcją wektorową. Wówczas istnieje rozwiązanie p: [fo — V > "H v\ —* Rⁿ zagadnienia początkowego

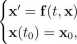
(URn-ZP)

Mi ’•••’ M_r

gdzie r) = min{<5, jfc,..., j^},

Mi = sup{ | fi(t, x) | : t G [t₀ — 5, t₀ + S], x G P }.

Odtąd aż do końca bieżącego podrozdziału zakładamy, że —oo < a < b < oo, —oo < Ci < di < oo, oraz

f: (a, b) x (ci, di) x ■ • • x (c„, d_n) —> Rⁿ jest ciągłą funkcją wektorową.

Definicja. Rozwiązanie p\ (a, /3) —> Rⁿ układu równań różniczkowych x' = f(t,x) nazywamy nieprzedłużalnym w prawo, gdy nie istnieje rozwiązanie (a,/3) —> Rⁿ układu, takie, że (3 > (3 oraz p = p na (o:,/?). Analogicznie, rozwiązanie p: (a,/?) —> Rⁿ układu x' = f(t,x) nazywamy nieprzedłużalnym w lewo, gdy nie istnieje rozwiązanie Żp: (a, fi) —> Mⁿ układu, takie, że a > a oraz ip = <p na (a, (3).

Rozwiązanie nieprzedłużalne to rozwiązanie równocześnie nieprzedłużalne w prawo i nieprzedłużalne w lewo.

Twierdzenie 6.4 (Twierdzenie o przedłużaniu rozwiązań). Niech ip: (a, fi) —> Rⁿ będzie nieprzedłużalnym w prawo rozwiązaniem układu równań różniczkowych x' = f(£, x). Wówczas

a)    P = b, lub

b)    Dla każdego zbioru zwartego K zawartego w (ci, d\) x • • • x (c_n, d_n) istnieje r G {a,P) takie, że p(t) ^ K dla każdego t G [t, P).

Niech <p: (a,P) —* Rⁿ będzie nieprzedłużalnym w lewo rozwiązaniem układu równań różniczkowych x' = f(t, x). Wówczas

a)    a = a, lub

b)    Dla każdego zbioru zwartego K zawartego w (ci, di) X • ■ • X (c_n, d_n) istnieje t G (a,P) takie, że p(t) K dla każdego t G (a, t\.

Część b) niekiedy formułuje się w następujący sposób: (t, p(t)) dąży, gdy t P~, do brzegu zbioru (a, b) x (ci, d\) x • • • x (cn, d_n) (odpowiednio:

(t, p{t)) dąży, gdy t —> a⁺, do brzegu zbioru (a, b) x (ci, d\) x • • • x (c_n, d_n)). Dowód twierdzenia o przedłużaniu dla układów jest dość żmudny, choć wykorzystywane są w nim tylko standardowe fakty z rachunku