74 75

4

kłowe u_ftb obliczymy, rozwiązując układ równań hybrydowych . drzewo Ba-laozone grubą linią na rysunku 3*2

^R1ⁱl -    = "*2

Rgij +    * -e, + «₂

+ i, - i₂ = -J₂ (pęk 9)

°3^U3 ⁼ J1’ ^u3 ^{= R}3^{J a 16} Y

Po wyeliminowaniu 1₁ oraz i₂ obliczamy napięcie a^, a następnie to

^aU^ul* * ^G1^(u4 " *2^J " °2⁽"^u1 ” *1 ⁺ mZ^{) =} -J2

-J₂ ♦ _Gle₂ + G₂e₂ -

⁺

1

1 ^T “2

U_M ł ts ^{+ U}if

16 ♦ 12 -

I -6 V

6 = 22 V

Rezystancja "wzierna del napięcia zwarciami, osi

^Rab - ^H3 ♦ G₄“V a ~;~Vł₂ =^ + 2=6®

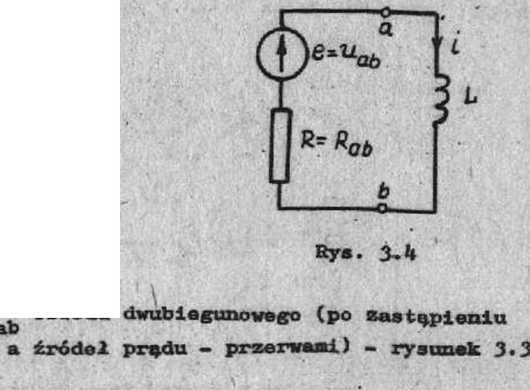
Ponieważ zastosowanie twierdzenia Theven±na polega na zastąpieniu odu rezystancyjnego równoważną gałęzią (e, R) - rysunek 3.4, szukany 1 i Jest rozwiązaniem prostego równania różniczkowego

^L 3T ♦ Keb¹ »

ab*

i(O) = O

(1)

i - •~^ptu^pt - o . Jg o - •-^t/T)

11

gdz i<

-^pti

)d-c

E ^u«b

ab

[a]    - s tai a. ci0jova

i =

U *

Oczywiste Jest, ż© wielkość    określa prąd ustalony elementu L,

^Kab

omyli prąd płynący w gałęzi zwierającej bieguny a b

ab

ab

i(*0 - _t

ab

2) Niezależnie od wyniku analizy w punkcie l)_t posłużymy się twierdzeniem w wersji Hortona, przy ozym prąd zwarcia i_Rb obliozymy po rozwiązaniu obwodu metodą napięć konarowych.

Obwód ze zwartymi biegunami posiada tylko 1 konar o nieznanym napię. oiu u£, ponieważ u' = -u£ - e ₁.

Dla pęku 9* s {R^, R₁, R^, Ry J₁] mamy następujący bilans prądów:

G|,u£ + G.,(u£ - *₂) ♦ G₂(u£ + «₁ - *₂> ♦ ,0₃(u£ + «,) + d, ♦ d₂ = #    ”^J1 " ^J2 * °1°2 * °2*®2 “ ®1^ł * °3®1    ^0 „

^u* -a,, ;¹ b, v a₂ + a₃-^Ł----? ^v

a więo prąd zwarcia wynosi

i_ab * G^(u£ +    ⁺ Ji ⁼    "3 ♦ 12) + 4 = -^ A (jak wyżej)

%

Kondukt anc Ja "wzierna"

Uproszczony dzięki zastosowaniu twierdzenia Hortona obwód przedstawili rysunek 3-5₉ a więc szukana, napięoie jest opisane równaniem

(2)

♦ ^G^>^a * ⁱ*b’ ^u<0) =