76 (120)

150

: równania statyki

letodzie poprzedniej.

Oslszy ciąg rozwiązania jest Identyczny jat

II.1.21. Oednośrednicowy pręt stalowy utwierdzony obu końcami w sztywnych i nieprzesuwnych ścianach obciążono układem sił skierowanych wzdłuż jego osi, tak Jak ilustruje to rys. 11.21. Obliczy.! minimalnę wartość średnicy pręta. Jeśli: P ■ 20 • 10³ N, 1 ■ 0,06 m, k = 80 MPa, k - 100 MPa.

Odpowiedź:

°min

■ 19,2f

p p

4-

Rys. 11,21

II.1.22. Trzyśrednicowy pręt miedziany utwierdzony obu końcami w sztywnych i nieprzesuwnych ścianach obciążono układem sił skierowanych wzdłuż Jfego osi, tak Jak ilustruje to rys. 11.22. Obliczyć maksymalne wartości naprężeń rozciągajęcych 1 ściskających w pręcie oraz przemieszczenia punktów A i B pod wpływem obciążenia. Dane: P > 260 000 N, d o = 40 mm, 1 - 160 mm, E = 1,1 • 10⁵ MPa.

Odpowiedź:

= 78,02 MPa; ■ 149,3 MPa.

⁷7^7?

Obniżenie punktu A wynosi 0,104 mm, natomiast punktu B 0,217 mm.

Rys. 11.22

II.1.23. Sztywna płyta prostokątna o ciężarze a ■ 200 k cowena przegubowo w punkcie A 1 zawieszona na dwóch prętach kroju F « 800 mm² Jest obciężona siłę P ■ -j- a oraz momentem (rys. II. 23a). Obliczyć naprężenia w prętach i kęt obrotu pod wpływem obciężenia. Pozostałe dane: a • 3 a, moduł You materiału prętów E » 2,1 • 10⁵ MPa.

o prze-M_c - Pa płyty nga dla

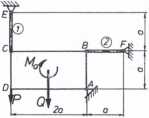
a)

b)

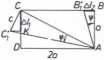
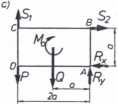
11.23

Rozwiązanie

Zakłada się, że oba pręty 1 i 2 sę rozciągane, zatem płyta obróci się dokoła przegubu stałego zgodnie z kierunkiem trygonometrycznym o pewien kąt ę>(rys. Il.23b). Tory ruchu punktów B i C można z pewnym przybliżeniem zastąpić odcinkami BB^ i CCj normalnymi do odpowiadających i promieni A8 i AC. Pręt 1 musi wydłużyć się o 4 1j i obrócić wokół przegubu E, tak aby Jego dolny koniec znalazł się w punkcie C^. Obydwa pręty wydłużą się, zatem są rozciągane siłami Sj i S₂ (rys. II.23c). Równanie sumy momentów działających względem punktu \ pozwala powiązać wartości tych sił bez wprowadzania innych - iadomych