90 (50)

2.2. Zmienne losowe dwuwymiarowe

Jeśli Aj, AA,, .....X_n są zmiennymi losowymi, to wektor

(" X j'

X ~~ i ^A 2

i ■

jest wektorem losowym lub, nazywając inaczej, /i-wymiarową zmienną losową (łub łączną zmienną losową). W zagadnieniach geodezyjnych każdy wynik pomiaru może być traktowany jako oddzielna zmienna losowa. Zazwyczaj opracowuje się zbiory wielu obserwacji (np. w problemach wyrównawczych). Na ogól mamy więc do czynienia z wielowymiarową zmienną losową.

Zmienne losowe wie! o wymiarowe można umownie podzielić (podobnie jak zmienne jednowymiarowe) na zmienne typu skokowego i zmienne ciągłe. Szczególnym przypadkiem zmiennej losowej a-wymiarowej jest zmienna dwuwymiarowa (Aj >j, tzn.

r x 11	i x
i * 1	lub X = |
L^A2.j	L ^

X =

X,

Dwuwymiarowa zmienna losowa (A^r, )j jest typu skokowego wówczas, gdy zarówno zmienna X, jak i zmienna Y przyjmują wartości ze skończony cli lub przeliczalnych zbiorów, tzn. X = ,V|, .xo,.v„, Y ~ vj,    y_m. Punkt

o współrzędnych (.v., y.) jest punktem skokowym zmiennej losowej (X. Y).

Prawdopodobieństwo, że zmienna losowa (X, >0 przyjmie parę wartości (x_i, y_;), zapiszemy w postaci (rys. 2.1.1)

P(X =_Xl, Y - yj) = pjj    (2.20)

przy czym

n m

XX

*'-i >“i

PU, <X< x,_r y, <Y <?„,)■■

lub    P(~™> < X <    - OO < y < 4o«) —    Pjj ~ ]

i i=i

gdy zmienne X i Y przyjmują wartości ze zbiorów nieskończonych, lecz przeliczalnych.

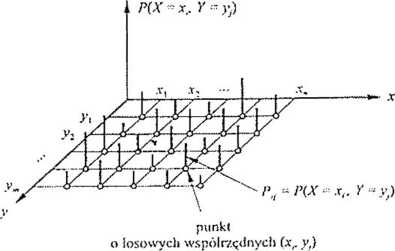
Rys. 2.11

Rozkład prawdopodobieństwa zmiennej skokowej (X, Y), a więc zbiór

wartości prawdopodobieństw Pij » ‘~ l.....ⁿ- J~ b    można również

przedstawiać w postaci tabelarycznej, np.

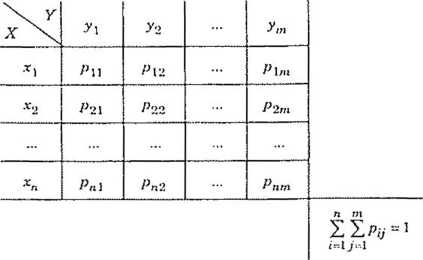
Dwuwymiarowa zmienna losowa (X, Y) jest typu ciągłego wówczas, gdy dla zmiennych losowych X i Y, przyjmujących wartości rzeczywiste, istnieje taka nieujemna i całkowalna funkcja    że

+«»+<*>

P{—°O < X < -ł-OO, — oo < Y <    — J J /(x, y) dx dy = 1    (2.21)

Jeśli zmienna X przyjmuje wartości tylko z przedziału (a_t,6_x), natomiast zmienna Y wartości tylko z przedziału (a._y, b_y ), to

p(—oo < X < +oo, — ©o < Y < +°°) = P(a_x < X < b_x, a_y < Y < b_v) =

V^;v

= j J/U, y)dxdy = 1

<V'y

91