CCF20130221056

IMccIiiini/in II. Trzy linie nieciągłości prędkości oddzielające obszary (I, II, III) j przemieszczające się z różnymi prędkościami (rys. 12.3). Na rysunku 12.3b pokazano hodograf, gdy obszar I jest nieruchomy. Wtedy obszar II porusza się z pręd kością V\2, a obszar IM z ko- Na rysunku 12.3c pokazano hodograf, gdy obszary poruszają się kolejno z prędkościami: V\, V₂ i F₃. Skoki prędkości wzdłuż linii nieciągłości prędkości są nachylone do nich pod kątem ę .

4.    OKREŚLANIE SIŁ NIEZBĘDNYCH

DO REALIZACJI ZAŁOŻONEGO MECHANIZMU

Siłę potrzebną do uruchomienia założonego mechanizmu kinematycznie moź liwego można określić za pomocą dwóch metod: metodą równowagi bloków i energetyczną. W obu przypadkach najpierw proponujemy mechanizm kinema tycznie dopuszczalny, polegający na wzajemnym ruchu sztywnych bloków, a następnie rysujemy hodograf prędkości.

Następnie, w metodzie równowagi bloków (stosowaną niezależnie od przyjęte go prawa płynięcia - stowarzyszone czy niestowarzyszone) analizujemy siły dzia łające na kolejne bloki. Brakujące składowe wylicza się z warunku równowagi elementu.

W metodzie energetycznej do wyznaczania sił niezbędnych do uruchomienia założonego mechanizmu korzystamy z warunku równowagi mocy obciążeń zewnętrznych i mocy wewnętrznej, dyssypowanej na liniach nieciągłości (1) (metodę tę można stosować jedynie dla prawa stowarzyszonego).

Obie ww. metody są równoważne i wyznaczone siły muszą być sobie równe. Poszukujemy natomiast mechanizmu dającego najniższe oszacowanie siły niezbędnej do jego uruchomienia. Przyjęty mechanizm deformacji jest dowolny i musi jedynie spełniać warunki kinematyczne. Poszukujemy jednakże mechanizmu dającego najniższe oszacowanie siły niezbędnej do jego uruchomienia, gdzie istotną rolę odgrywa doświadczenie osoby oraz badania eksperymentalne.

5.    WYZNACZANIE STATECZNOŚCI SKARPY

METODĄ MECHANIZMÓW KINEMATYCZNIE DOPUSZCZALNYCH

5.1. Zastosowanie metody mechanizmów kinematycznie dopuszczalnych do analizy stateczności skarp

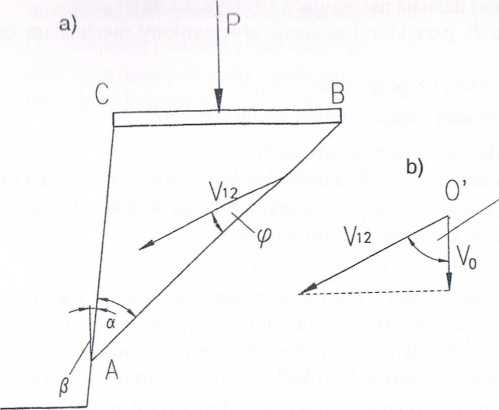
Rozpatrzmy przykładowo zagadnienie granicznego obciążenia skarpy (płaski stan odkształcenia) o kącie nachylenia /?(rys. 12.4a) i załóżmy, iż wskutek obciążenia P zostanie uruchomiony mechanizm składający się z ruchu sztywnego bloku ACB wzdłuż linii płaszczyzny AB nachylonej do skarpy pod kątem a. Ponieważ pozostała część skarpy jest nieruchoma, A4BC osuwa się z prędkością F_l2 nachylo-

lit) do linii nieciągłości Ali pod kipom <p. W tym przypadku hodograf składa się / jednego wektora V\2, którego składową pionową oznaczono jako F₀ (rys. 12.4b).

a+p+<p

d)

c)    P

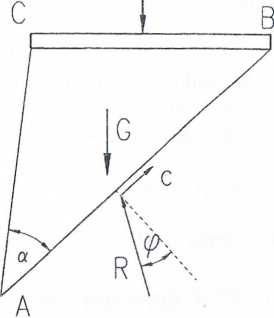
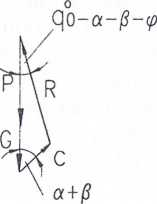
Rys. 12.4. Prosty mechanizm kinematycznie dopuszczalny dla zagadnienia granicznego obciążenia skarpy

a) prędkości na linii nieciągłości dla skarpy, b) hodograf dla mechanizmu zniszczenia skarpy, c) siły działające na sztywny klin w stanie granicznym, d) wielobok sił

W rozwiązaniu poszukujemy kąta a, który daje nam najniższe oszacowanie sity /’. Można to zrobić numerycznie (dla bardziej złożonych zagadnień) lub analitycznie określając ekstremum pochodnej funkcji względem a.

109