CCF20120509039

£UU Lzęsc ii. Rozwiązania i uupowieuzi

czyli mierzona prędkość przepływu płynu

”" = V²7^!"'-

3.1.13. Układamy równania Bernoulliego dla przekrojów: 1-2,1-3 i 1-4, względem poziomu fundamentu, a zatem:

(D

(2)

(3)

c\    Pi    c\    p_h

—-H---1~ ph —    ---b ga,

2 p    2 p

ci , Pi .    , c\p_h

2    p    2    p

—-H---\~ gh — — H---b 3ga.

2    p    2    p

Z przedstawionych równań wyznaczamy prędkość wypływu. Ponieważ prędkość opadania zwierciadła cieczy w zbiorniku c_t = 0, więc:

Pi-Pb

+ g{h - a)

‘3=    2

c_A = 12

Pi-Pb

+ g(h — 2 a)

Pi ~ Pb L P

+ g(h — 3a)

Prędkość c w przewodzie doprowadzającym określimy z warunku ciągłości:

cA_x = c₂A + c₃A + CąA ,

w którym c₂, c₃ i c₄ są prędkościami opisanymi wzorami (4), (5) i (6).

Ostatecznie

c = — (c₂ + c₃ + c₄).

^Ai

3.1.14. W równaniu Bernoulliego dla przekrojów 1 i 2

c\ P-y    „ Cl P,

-^ + ^ + O = ^ + ^ + 0_Z 2    p    2    p

(4)

(5)

(6)

(7)

(8)

O)

ciśnienie

Pi = Pi= Pb>

stąd

Z równania ciągłości

c_xnr²

= c₂

nd²

~T

wyznaczamy zmienną prędkość

- ^4c‘^

i podstawiamy ją do zależności (2), skąd otrzymamy

^16c'd* ⁼ c2l+2gz’

a po przekształceniu

z

2.0

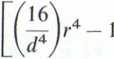
3.1.15. Zgodnie ze wzorem Torricellego, prędkości wypływających strun (rys. 1-3.14) wynoszą:

= Jlę)(h-y_x),

^c2 = s/ig(h-y₂)-

Z równań ruchu wynikają następujące zależności: dla otworu górnego

	^xi ^= ci	11, ki = 20fl
czyli	i *i kl =20-1	1 U 2 ^2kl^Cl lub x\ = —-
	ci	0
oraz dla otworu dolnego
	x2 = c2\	y2 = 20t2
skąd
	j. *1 y 2 = 2 0 2	i u 2 ^2yzc\ lub x2 =-
	C 2	0

Z warunków zadania wynika, że

wobec tego, porównując równania (2) i (3) oraz podstawiając zależności (1), otrzy m wyrażenie: