CCF20130221059

Nji przezroczystej kalce (z zaznaczonym układem odniesienia x y) rysujemy zarys skarpy (rys. 12.5 - BC = 100 mm, CD = 300 mm).

Obciążamy trzonek ubijaka kładąc na niego kolejne ciężarki do momentu osunięcia się skarpy (pionowy ruch ubijaka jest ograniczony do długości 15 mm). Wiedząc ile wynosi masa ubijaka (12) i ciężarka (13) oraz znając masę ciężaru, przy której nastąpiło osunięcie skarpy określamy siłę krytyczną P (rys. 12.5), przy której został uruchomiony mechanizm poślizgu. Na przezroczystej kalce zaznaczamy (linią ciągłą) linię poślizgu ośrodka (rys. 12.5 - BA).

Zakładając, iż mechanizm zniszczenia skarpy polega na ruchu sztywnego bloku wzdłuż linii prostej (płaszczyzny, wychodzącej z tylnej krawędzi ubijaka) oraz korzystając z metody równowagi bloków i z metody energetycznej określamy siłę krytyczną P (równania (12.2) i (12.3)) dla kąta nachylenia linii poślizgu a i stałych materiałowych: <P> - 24°, y= 18,4 kN/m³, c =.......kN/m² (wartość wyznaczona eks

perymentalnie) oraz wymiarów skarpy: szerokość skarpy = 320 mm, początek powierzchni poślizgu = 100 mm (rys. 12.5 - BC).

Korzystając z zależności (12.5) lub (12.10) dla danego mechanizmu poślizgu wyznaczamy analitycznie (lub numerycznie - wykres) kąt a = a_mj_n, dla którego określana siła krytyczna jest minimalna P = P_m\_n.

Wyniki obliczeń (a_mj_n, ,P_mjn) porównujemy z rezultatami doświadczenia, rysując obliczony zarys linii poślizgu na tle linii poślizgu wyznaczonej eksperymentalnie oraz porównując teoretyczną i eksperymentalną siłę krytyczną (rys. 12.5).

6. WYZNACZANIE METODĄ MECHANIZMÓW KINEMATYCZNIE DOPUSZCZALNYCH SIŁY GRANICZNEJ DLA ZAGADNIENIA NAPORU PŁASKIEJ ŚCIANY

6.1. Zastosowanie metody mechanizmów kinematycznie dopuszczalnych do analizy zagadnienia naporu ścian

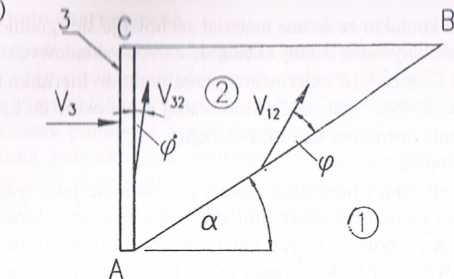
Rozpatrzmy przykładowo zagadnienie naporu przesuwanej poziomo pionowej ściany w płaskim stanie odkształcenia (rys. 12.7) i załóżmy, iż zostanie uruchomiony mechanizm składający się z ruchu sztywnego bloku ACB wzdłuż linii (płaszczyzny) AB nachylonej pod kątem a.

Aby móc narysować hodograf, należy najpierw określić warunki na linii kontaktu pomiędzy ścianą a gruntem (linia AC). Zazwyczaj przyjmuje się, iż na linii tej materiał zachowuje się zgodnie z prawem Coulomba

|r„| = c* + cr„-tg^*,    (12.11)

z tym, iż zarówno spójność, jak i kąt tarcia wewnętrznego są inne aniżeli dla ośrodka, w którym c ź c, cp* * tp. Wartości te należy określić doświadczalnie, pamiętając że tgę = ju, gdzie // jest współczynnikiem tarcia ośrodka o ścianę.

c)    d)

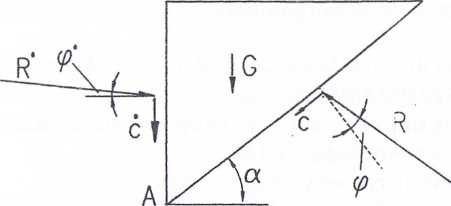
Rys. 12.7. Prosty mechanizm kinematycznie dopuszczalny dla zagadnienia naporu ściany

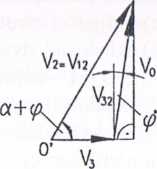
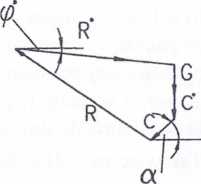
a) prędkości na linii kontaktu ściana - grunt, b) hodograf, c) siły działające na klin ABC, d) wielobok sił

Na rysunku 12.7b przedstawiono hodograf dla tego zagadnienia. Z punktu O rysujemy wektor V₃ odpowiadający prędkości przesuwu ściany. Ponieważ prędkość ośrodka V\ = 0, to V₂ = V\₂ i z punktu O rysujemy prostą o kierunku wektora Vi = V]₂. Z końca wektora V₃ rysujemy prostą o kierunku wektora V₃₂ aż do przecięcia z prostą o kierunku wektora V₂. Punkt ich przecięcia wyznacza końce wektorów V₂ ~ V\₂ i Z32.

6.1.1. Metoda równowagi bloków

W stanie granicznym na sztywny klin ABC (przyjmując szerokość skarpy równi) jednostce długości) działają następujące siły (rys. 12.7c):

a)    siła oddziaływania ściany,

b)    ciężar własny klina G (pole AABC-y ),

c)    reakcja nieruchomej części ośrodka wzdłuż linii AC,

d)    reakcja nieruchomej części ośrodka wzdłuż linii AB.

115