CCI20130725125

127

7.5. Modele osadu czynnego

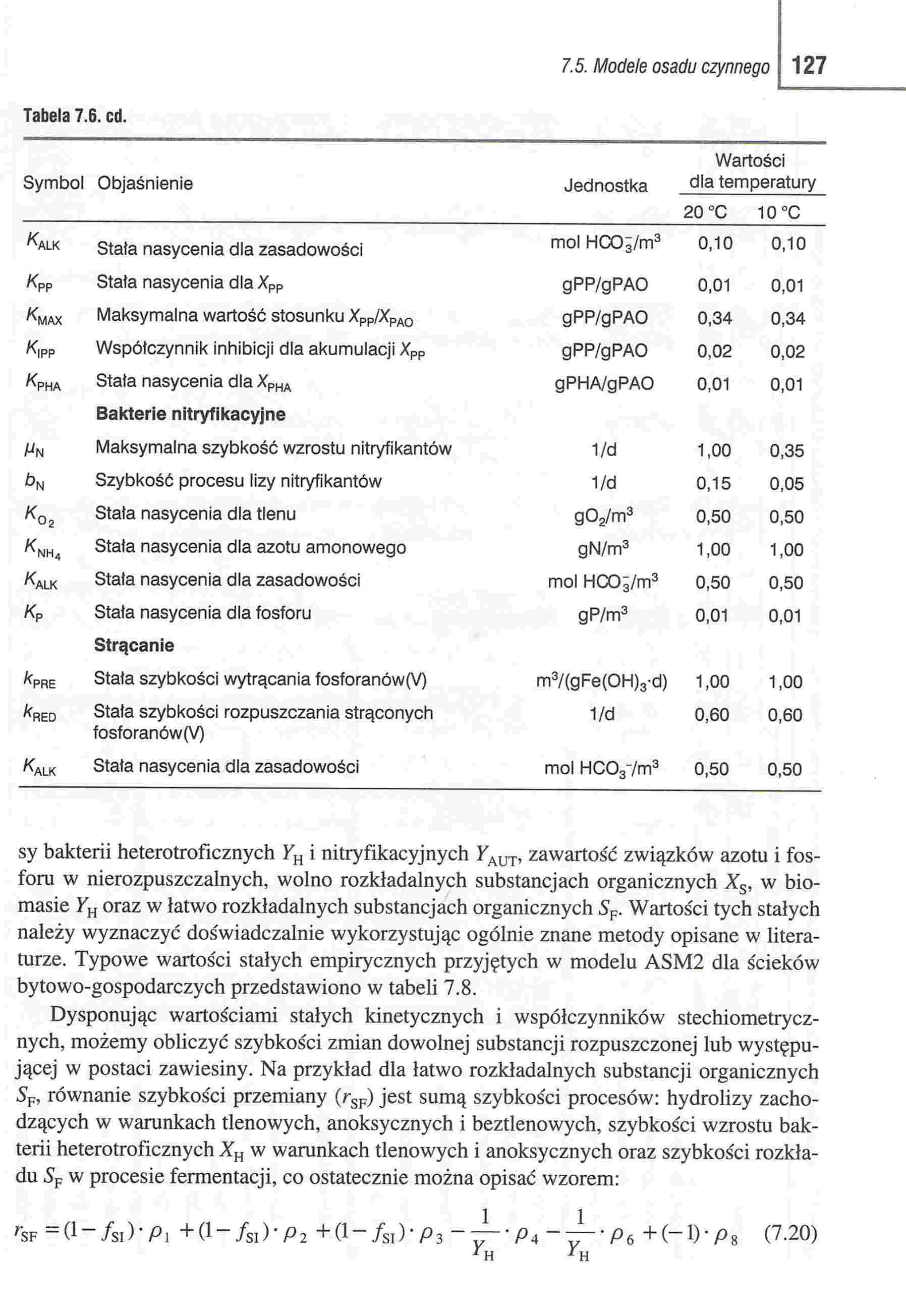
Tabela 7.6. cd.

Symbol	Objaśnienie	Jednostka	Wartości dla temperatury 20°C 10°C
Kalk	Stała nasycenia dla zasadowości	mol HCOg/m^3	0,10	0,10
KpP	Stata nasycenia dla XPP	gPP/gPAO	0,01	0,01
^MAX	Maksymalna wartość stosunku XPP/XPA0	gPP/gPAO	0,34	0,34
k|Pp	Współczynnik inhibicji dla akumulacji XPP	gPP/gPAO	0,02	0,02
kpHA	Stała nasycenia dla XPHA Bakterie nitryfikacyjne	gPHA/gPAO	0,01	0,01
V N	Maksymalna szybkość wzrostu nitryfikantów	1/d	1,00	0,35
ÓN	Szybkość procesu lizy nitryfikantów	1/d	0,15	0,05
Kn °2	Stała nasycenia dla tlenu	g02/m^3	0,50	0,50
	Stała nasycenia dla azotu amonowego	gN/m^3	1,00	1,00
^ALK	Stała nasycenia dla zasadowości	mol HCOj/m^3	0,50	0,50
KP	Stała nasycenia dla fosforu Strącanie	gP/m^3	0,01	0,01
kpRE	Stała szybkości wytrącania fosforanów(V)	m^3/(gFe(OH)3-d)	1,00	1,00
^RED	Stała szybkości rozpuszczania strąconych fosforanćw(V)	1/d	0,60	0,60
Kalk	Stała nasycenia dla zasadowości	mol HC037m^3	0,50	0,50

sy bakterii heterotroficznych k_H i nitryfikacyjnych k_AUT, zawartość związków azotu i fosforu w nierozpuszczalnych, wolno rozkładalnych substancjach organicznych X_s, w biomasie Y_h oraz w łatwo rozkładalnych substancjach organicznych S_F. Wartości tych stałych należy wyznaczyć doświadczalnie wykorzystując ogólnie znane metody opisane w literaturze. Typowe wartości stałych empirycznych przyjętych w modelu ASM2 dla ścieków bytowo-gospodarczych przedstawiono w tabeli 7.8.

Dysponując wartościami stałych kinetycznych i współczynników stechiometrycz-nych, możemy obliczyć szybkości zmian dowolnej substancji rozpuszczonej lub występującej w postaci zawiesiny. Na przykład dla łatwo rozkładalnych substancji organicznych S_F, równanie szybkości przemiany (r_SF) jest sumą szybkości procesów: hydrolizy zachodzących w warunkach tlenowych, anoksycznych i beztlenowych, szybkości wzrostu bakterii heterotroficznych X_H w warunkach tlenowych i anoksycznych oraz szybkości rozkładu S_F w procesie fermentacji, co ostatecznie można opisać wzorem:

^rSF ⁼0 ^— /si)' Pi + (1^— /si)' Pi "1" 0 7si) ’ P3 ^— 77~" P^ ~ 7T~' Pe +    1)' Ps (7.20)