DSC07107 (5)

144

Badanie funkcji

b) Zauważmy, ze 3z^ł > O dU dowolnego z^O. Zatem

p(0) =4 > 4 - 3x¹⁰⁰

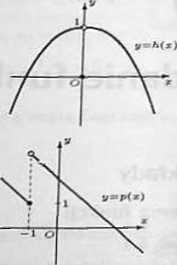
dla każdego x ?£ 0. co oznacza, ie funkcja *7 ma w punkcie zo = 0 maksimum lokalne wlaśdwe (rysunek),

c) Ponieważ A(0) = 0, więc

A(x) = 1 — x^a > A(0)

dla każdego x spełniającego nierówność 0 < W < 1, co oznacza, że funkcja A ma w punkcie xo = 0 minimum lokalne właściwe (rysunek).

d) Mamy p(—1) = 1, więc

PM = -*>P(-“i)

dla x < -1 oraz p(x) = 2 - x > p(-I) dla —1 < x < 1. Zatem p(x) > p(—1) dla 0 < fx — (—1)| < 2, co oznacza, że funkcja P ma w punkcie xo = — 1 minimum lokalne właściwe.

• Przykład 6.2

Znaleźć wszystkie ekstrema lokalne podanych funkcji:

•>/(*>« 22?-I5i? + 3ftt; b)_fl(*) = -5^_;    c)A(*) = x';

^d) <?(x) = minx + *”^^2ł;    o) p(x) = x*; f) r(x) = x- tfx.

Rozwiązanie

Phnkcja może mieć ekstrema lokalne tylko w punktach, w których jej pochodna równa się zero albo w punktach, w których pochodna nie istnieje. W punktach, w których pochodna *^en,j®» rodzaj ekstremum (maksimum, minimum) ustalamy badając zmianę znaku tej Pochodnej lub też określając znak pierwszej niezerowej pochodnej parzystego rzędu,

a) Dla /(*) = 2z*- l&r* + 36x mamy /(*) = 6x^a-3Gr + 36. Ponieważ badana funkcja Puchodną w każdym punkcie prostej, wiec może mieć ekstrema tylko w tych punktach, w których jfcfr « 0- Tak więc

/(x) W 0 <=> óx³ - 30z + 34 = 0 *=» 6(x - 2)(x - 3) - 0 <—* x - 2 lub x =* 3.

Przykłady

145

Mamy następnie /"(*) = 12* — 30, więc / (2) = -6 < 0, /"(3) > 0 . Rozważana funkcja na żalem w punkcie * = 2 maksimum lokalne właściwe równe 28, a w punkcie * = 3 minimum lokalne właściwe równe 27.

b) Dla g(x) =    mamy

*^a -f 4 - * • 2* A-z*

⁹ (X)    (**+4)^a    = (*^a+4)^a-

Ponieważ badana funkcja ma pochodny w każdym punkcie prostej, więc może mieć ekstrema jedynie w tych punktach, w których g'{x) = 0. Tak więc

g(z) = 0

— *^a = 0 <=> * = -2 lub x = 2.

•1 -z*

■ (*^a+4)³

Zbadamy teraz znak pochodnej na przedziałach (-oo,—2), (—2,2), (2,oo). Mamy f •! -** > 0 dla * € (-2.2),

\ 4 - z³ < 0 dla * 6 (—oo, —2) U (2, oo).

Zatem

g (z) < 0 dla z € (—oo, —2) g'(x) > 0 dla * € (-2,2),

</(*) < 0 dla * € (2,oo).

Tak więc w punkcie —2 pochodna zmienia znak z ujemnego na dodatni, czyli w punkcie tym funkcja g ma minimum lokalne właściwe równe —natomiast w punkcie 2 pochodna zmienia znak z dodatniego na ujemny, czyli w punkcie tym funkcja g ma maksimum lokalne właściwe równe —.

4

c) Funkcja h(x) = *^x jest określona dla * > 0. Ponadto pochodna h\x) = (1 + In*)** (zobacz Przykład 4.10 d)) jest również określona dla * > 0. Fbnkcja h może mleć ekstrema tylko w tych punktach, w których h'(x) = 0. Tak więc

1 + In* = 0 <=> x = -.

(1 + lnx)x* = 0

h\x) = 0 Mamy następnie

h'\x) = (1 -f In*)'** + (1 + In*)(**)^/ =    + (1 + ln*)(l + In*)**,

więc

.1

Oznacza to, że funkcja h ma w punkcie z = - minimum właściwe lokalne równe

d) Funkcja q(x) = sin z +    ma okres podstawowy T = 2x, zatem jej ekstrema

wystarczy znaleźć tylko na przedziale (0,2jt). Mamy