DSCF2552

192

6. Zmacam losowe jedaowyraaaro^r«e

| 6.1. Zmienna Imesma j po^ek rozkłada swiauilopodohirńu

193

P(X=u

—¹ im irr ycfa od xj

U.7. Funkcję

6.13)

i Ffx>= j fitydi

(6.l.6a)

rej zachowanie sag zależy od przypadkowego dobom punktu x) znajdzie się w przedni. <0, ffjsrj). Można udowodnić, źe te przecrwobrazy jako podzbiory przedziafa /$j tworzą cóio borelowikie 5,

Zauważmy wraźcie, że spełniony jest związek

P(X<x)=i^,((?0)<x)= /*(y < Fix))=F(x),

co dowodzi, że dytryfaoanta zmiennej losowej X jest właśnie funkcja ćTx).

Dgggq& 6.l.di Zmłinpw fiwpyg skokmą flazywggjy.igfcą zsjEgprig i ysową X, dla toąą istnieje frakcja jP{X=xj)=jfc>0 (k=0_r 1,2,.,.) taka, źe dla każdego rzeczy% zachodzi relacja

IklJ)    f(x)= J P(X=x*),

tzn. P(X<TI nhłmT* qę nper sumowanie wszystkich praw<^ppdohTen>.r dla x» mniejszych Definicja 6.

P(X=x_t)=Pt

nazywam'/ funkcja Dra%domodobkmt^a znoengej losowej X skokoyei. warte wamr ptmkiani skokoKjmi. a prawdopodobieństwa p* — skokami.

Z definicji 6.1 J wynika, źe (6X4)

Jeżeli zmienna losowa skokowa X przyjmuje wartość 6, to

(6.1.5a>    lPla<X^b)=F{b)-Fla)+PiX=‘b). \

Dtftnkm 6.1.%! Zjniermą losową ciągłą nazywamy zmienna losową X. dla której ;_?trtae-je taka nieujemna funkcja f (x)_t że dla każdego rzeczywistego z zachodzi reiaci

■»

(6.1.6;

Dewmcja- 6.1.9^ Eiinkcję f (x) spełniającą związek (6.1.6;, nazywamy gęst&uiią prawdo~ oodobieństwa albo po prostu zęstością zmiennej topornej ciągłej.

Mówimy, źe dany jest rozkład prawdopodnbiefuuta zmiennej losowej, jeś3ś znana jest dyifrybuama, względnie jeśli znana jest funkcja prawdopodobieństwa w przypadku zaafecnet    skokowej lub gęstość w przypadku zrffff**"^ loyywęj ciągłej,

[(y> jest fgnkcracią^ą w punkcie x. to zachodzi związek_____

F'(x)=fix)₉ czyh z defioky pochodnej, w punkcie ciągłości

. F(jc+4x)-F(jrt    F(x<X<x+dt)

}{%}— nm-—s= nu —----

Jkx-~H Ax    Ax

>ę*f Na odwrót-.kaźda funkcja /(xy rzeczy wata. niecjenma, całkowalna na os* Ox od —x ido +x i spełniająca związek.

Funkcję prawdopodobieństwa można podać w postaci wzoru lob tabeli, T sposób jest wygodny w przypadłoś, gdy zmienna losowa przyjmuje skończ/ wartości. Wykoajeroy wtedy dwuwierszową tablicę, w której górny wiersz za ~ tkie wartości zmiennej losowej w dowolnym porządku, najczęściej jednak według wartości, a dolny — odpowiadające im prawdopodobieństwa. Jeżeli np, zmień:. i przyjntBje wartości x_;, x₂,^z odpowiednimi prawdopodobieństwami p_:. |o można ją scharakteryzować w postaci tabficy 6X1.

ec .“sani I ma liczbę I era wizytr I rosaąs* I

L'/./łSl X I

(6,1.7)

f f(x)dx=\

Tablica 6X1

_    r—

PiX»xO

Pt

Pi

a

Zauważmy, że

P(a<X<b)s* £ F(X=x._e)_r

/ęŚZtjeć&M

a po awzgfedniewBii wzoru 6X2 otrzyinujeiny

jest gęstością zmiennej losowej X typu danego-.

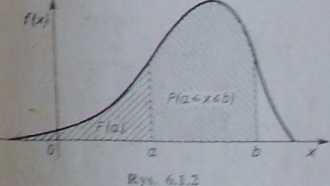
Modelem dla zmienny losowej ciągłej może być np. popdarw „koło szczęka". Strzałka może wskazać każdy padu okręgu, jednak prawdopodobieństwo, że strzałka zatrzyma się na wybranym uprzednio punkcie, jest równe 2ens, ponieważ punktów, na których strzałka może się zatrzymać, jest nie-kończenie wiele. W tym przypadku nie ma cela pytać o prawdopodobieństwo, że zmien-_ na losowa przyjmie pewną określoną wartość, ale należy pytać o prawdopodobteń-że zmienna losowa przyjmie wartość mniejszą (większą) od z góry ustalonej liczby lub, że przypnie wartość z obranego przedziału. Korzystając z (6.1.1) r (6.1.6), otrzymujemy

. #

*6. IX)    F<flęX<k)«F(fe)-F(a)* J /(x)dx.

!ń wtiwiwwiiiii i n»