DSCF6587

130

Ponieważ układ fizyczny pozostawiony „samemu sobie” dąży do osiągnięcia stanu o minimalnej energii, wynika stąd, zgodnie ze wzorem 1, że siły napięcia powierzchniowego dążą do zmniejszenia powierzchni cieczy, Następstwem tego jest m. in. kulisty kształt kropel cieczy (jeśli można pominąć siły związane z grawitacją, naelektryzowaniem i in.), ponieważ minimalna powierzchnia ograniczająca daną objętość ma kształt kulisty.

2. Wioskowa tość

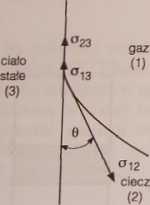
Rys. 35. Siły działające na granicy ośrodków

Rozpatrzmy zjawiska powierzchniowe zachodzące na granicy ciała stałego, cieczy i gazu (rys. 35). Działające tu siły, odniesione do jednostki długości „obwodu” powierzchni, równe są współczynnikom napięcia powierzchniowego o_l2, o_l3, a23. W warunkach równowagi powierzchnia cieczy przyjmuje kształt, dla którego wypadkowa tych sił nie ma składowej stycznej do ścianki:

ffi3 + ff23 = «r₁₂cos0    (5)

kąt 0 nazywa się kątem granicznym.

Ponieważ gazy nie wykazują niemal napięcia powierzchniowego względem ciał stałych pji.₃.3 0), kąt graniczny spełnia z dużą dokładnością związek:

cos 0 = —    (6)

012

W wypadku, gdy o-₂₃ = 0,0 = ń/2; nie istnieje oddziaływanie pomiędzy ciałem stałym i cieczą styczne do ścianki naczynia. Dla

ff₂3>0'l2,    0—*-0

ciecz tworzy wówczas cienką blonkę na powierzchni ciała stałego (przypadek całkowitego zwilżania). I tak np. dla wody i czystego szkła znaleziony doświadczalnie kąt graniczny ma wartość mniejszą od 2- 10^_3rad.

Po zanurzeniu kapilary do cieczy stwierdzamy, że poziom cieczy w rurce na ogół różni się od poziomu cieczy na zewnątrz. Różnicę wysokości określimy z warunku równości parcia słupa cieczy i składowej stycznej siły napięcia powierzchniowego:

_    .    , ,    2ff cosO

litra cos U = nr-pgh —*• h =- (71

pgr

W zależności od wartości kąta granicznego h jest dodatnie lub ujemne, 0. poziom cieczy w kapilarze podnosi się (np. woda w kapilarze szklanej) lub obniża (np. rtęć w kapilarze szklanej). Znając h można ze wzoru i wyznaczyć napięcie powierzchniowe. Jeśli przyjąć ponadto 0 = 0, co np. * przypadku wody jest bardzo bliskie prawdy, otrzymamy:

], Metoda pomiaru

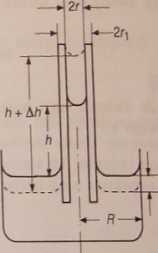
Doświadczenie polega na wyznaczeniu współczynnika napięcia powierzchniowego metodą pomiaru wzniesienia się słupka cieczy w kapilarze. Wyprowadzimy teraz zależność uwzględniającą, w odróżnieniu od wzoru 8, wpływ ścianek naczynia zewnętrznego (rys. 36).

bh

Rys. 36. Rysunek pomocny do otrzymania wzoru 17

Posłużmy się teraz zasadą prac wirtualnych, tzn. załóżmy, że układ znajdujący się w rzeczywistości w stanie równowagi, został z położenia równowagi nieznacznie „wychylony”. Uniesienie słupicą cieczy w kapilarze z wysokości h do h+Ah i związane z tym obniżenie poziomu cieczy w naczyniu wymaga wykonania pracy przeciwko siłom ciężkości:

(9)

Al/j = nr²pgh (A h — Sh)

W przypadku nieściśliwej cieczy o stałej masie przyrost objętości w rurce jest równy ubytkowi w naczyniu:

7cr²(A/r — Sh) = (kR² M itrj)Sh    (10)

W wyniku podniesienia się słupka cieczy w kapilarze powierzchnia styku jej wewnętrznej ścianki z powietrzem uległa zmniejszeniu o AS,:

A Sj = 27i r(Ah — Sh) OD