fizyka030

Równanie (7.1) jest odpowiednikiem równania II zasady dynamiki w ruje    ....

chu postępowym: a =    . Rolę przyspieszenia liniowego w ruchu obro

ni

towym bryły odgrywa przyspieszenie kątowe, rolę siły pełni moment siły. a rolę masy - moment bezwładności.

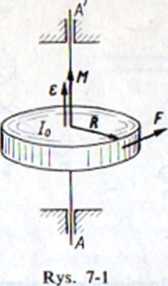
Przyspieszenie kątowe i moment siły są wielkościami wektorowymi. Są one skierowane wzdłuż osi stałej obrotu i są określone za pomocą iloczynów wektorowych¹ \ Moment siły oblicza się ze wzoru

M = Rx F , M = R± F = RF sin a    (7.2)

gdzie R_x jest odległością między osią obrotu a kierunkiem działania siły (zwaną też ramieniem siły). Na rysunku 7-1 wektory R i F są do siebie prostopadłe, więc R_x = R.

Momentem bezwładności bryły względem danej osi nazywamy sumę

H

iloczynów elementarnych mas m_h które tworzą bryłę o masie = £ ^mb

i

przez kwadraty odległości r_{ tych mas od danej osi, zatem

fl

/o = "», r]+m₂ r\ + ... +m. r\ s» £ m,r?    (7.3)

Im 1

Moment bezwładności ciała zależy nic tylko od wielkości masy wykonującej ruch obrotowy, ale także od sposobu rozmieszczenia tej masy wokół

*» Iloczynem wektorowym dwóch dowolnych wektorów a i b nazywamy wektor cm a y. b. prostopadły do wektorów a i b. Wartość liczbową wektora c obliczamy ze związku c = ab sin i, gdzie a jest to kąt między wektorami a i b. Zwrot wektora c określa reguła śruby prawoskrętnej. zatem zmiana kolejności składników w iloczynie wektorowym zmienia zwrot wektora c.

osi obrotu. Działając tym samym momentem siły M na bryłę o masie m uzyskamy większe przyspieszenie kątowe c, gdy masa bryły jest rozmieszczona bliżej osi (rys. 7-2a), mniejsze zaś, gdy masa jest rozmieszczona dalej

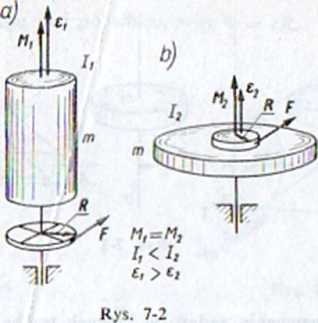
od osi (rys. 7-2b). W tablicach są zwykle podawane momenty bezwładności różnych regularnych brył względem osi symetrii przechodzących przez ich środek masy. Na przykład moment bezwładności:

/o = mR² - dla walca cienkościennego

/₀ = mR² — dla walca pełnego jednorodnego

A> = - mR² — dla kuli jednorodnej gdzie m — masa, a R — promień tych brył.

Dla pręta jednorodnego o masie m i długości / moment bezwładności względem osi prostopadłej do pręta i przechodzącej przez jego środek

wynosi:

^{/o =} ~J2 ^m,i

Jeżeli w zadaniach trzeba obliczyć moment bezwładności względem osi nic przechodzącej przez środek masy ciała, stosuje się wówczas twierdzenie Stcinera, które mówi, że moment bezwładności I_A bryły względem dowolnej osi AA' wyraża się wzorem

(7.4)

65

I_A — mRoA + Io

• ZOIÓr zadań z fizyki