hpqscan0004 (4)

Imię i nazwisko

Wyniki

1
2
3
4
6

®    = min{ f _Pi.

i=i

gdzie pj oznacza ii punktów uzyskaną z

Egzamin z matematyki dyskretnej. I rok studiów inżynierskich. I termin, 19 czerwca 2007.

Uwaga. Wszystkie rozwiązania powinny być bardzo dokładnie i w miarę możliwości formalnie uzasadnione. Rozwiązania poszczególnych zadań oceniane są jako całość. Na ocenę wpływa również sposób, poprawność i precyzja argumentacji. Duże błędy mogą dyskwalifikować całe rozwiązanie danego zadania, a błędy o charakterze zasadniczym mogą dyskwalifikować cały egzamin.

(15pt)

(lOpt)

(25pt)

o

1. Niech .4 będzie zbiorem skończonym. Niech

£q(.4) = (Eq(A); n,U^s((£q(ń)))

gdzie

U$s(eq(yi)) : Eq(A)² —> Łq(A) ((x, y) Jó(e_q(.4))(z U y)) będzie algebrą typu (2, 2).

Czy <£q(A) jest kratą? Jeśli tak to opisać jej własności?

2. Niech 21 = (A, <) będzie systemem relacyjnym, w którym relacja < jest liniowym porządkiem. Wykazać, że 21² = (A²; <²*) jest kratą dystrybutywną.

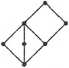
3. Diagram Hassego zamieszczony obok przedstawia pewną kratę £.

(i)    Znaleźć atomy i coatomy tej kraty.    (lpt)

(ii)    Czy krata £ jest dystrybutywną?    (lpt)

(iii)    Czy krata £ jest modularna?    (lpt)

(iv)    Czy diagram ten może być diagramem algebry Boole^:a?    (2pt)

(v)    Narysować diagram Hassego <£on(£).    (lOpt)

(vi)    Czy krata £ jest rozkładalna na produkt prosty? Jeśli tak, to przedstawić

jej rozkład.    (5pt)

(vii)    Czy krata £ jest rozkładalna na produkt podprosty? Jeśli tak, to przedsta

wić jej rozkład na produkt podprosty. Przedstawić na diagramie podproste zanurzenie.    (5pt)

4. Niech .4 będzie zbiorem (A -fi 0). Niech r, s G Eq(A). Określmy rodzinę relacji (20pt) (gi)i€N następująco:

go —A,    £?n+l

g_nr,    n G 2N,

g_ns,    n G 2N + 1.

Wykazać, że 8_e,A{r U .s) = (J p,;.