3582308037
WYKŁAD 25
CAŁKI KRZYWOLINIOWE
PRZYKŁAD 25.1
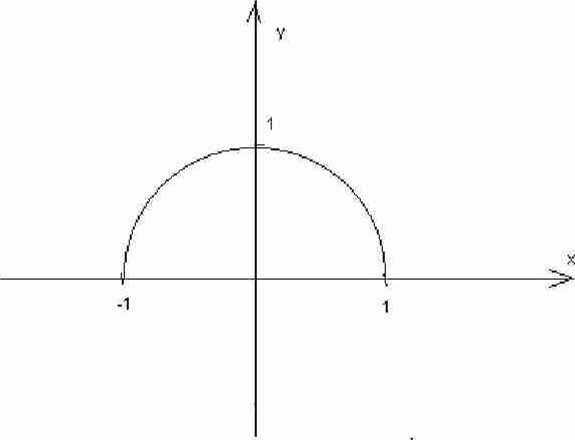
X2 +y2 =1 y SiO
. *:C0Sl
I: t«[o.r<
f sini
Taka parametryzacja okręgu zadaje nam kierunek przeciwny do ruchu wskazówek zegara
X: I
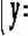
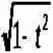
1
Wyszukiwarka
Podobne podstrony:
358 V. Funkcje wielu zmiennych W przytoczonym przykładzie pochodne x2+y2 { 8x2y2
Przykład: du dv du dv dx dy1 dy di /(z) = z ■ 2* = (x + iy)(x - iy) = x1 + y2 u = x2 + y2;v = 0;
wyklad 4 str 1 2 i Zdefiniuj pojęcie koszt mieszany. Podaj przykład 25. Zdefiniuj
DSC00084 (6) $ Przykład 3. l (x2 - y2 )dx + 2xydy = 0.
42 (78) Przykład 5. Wyznaczyć pole części walca o równaniu x2+y2=ax wyciętego sferą o równaniu:
105 4 X0. V2 , XI Y2. t X2 Y2. ; M99 (KONIEC PODPROGRAMU): __ 00300 (PRZYKŁAD UŻYC
Przykład Zbadać różniczkowalność funkcji /: R: -> RJ,/(.r, y)= (.ry, x+y, x2 + y2) w punkcie (.xo
568 XIV. Całki zależne od parametru Na przykład, nie oblicząjąc całek J In (x2+y2)dx, O widzimy od
38 (82) i (t c ot-r. / Irr 1 = ih I, « » Przykład 2. Obliczyć całkę: JJJ(x2 + y2 + 2z)dxdydz , v gdz
geo1 x X2=? X! Y, Y2=? Zad. 2 Obliczenie współrzędnych punktu Wyznaczyć: współrzędne X2, Y2 punktu 2
Image3097 df _ 1 1 ^arctg^ dX yi + {Ł)2 1 Y X ^arctg* 0 9 ® J y ^arctg* 3f _ X f ^arctg* X2 + y2 e
img033 33 f(*.y) • liln (x2.y2)’. f(x,y) « srccos , f(x.y) »
więcej podobnych podstron