3582320260

Przykładowy zestaw na pierwsze kolokwium z Badań Operacyjnych

1. J. Carpenter jest właścicielem sklepu z materiałami budowlanymi Pewnego dnia, bierze on udział w aukcji używanych materiałów budowlanych. Interesują go bloczki betonowe oraz deski podłogowe. Po obserwacji pierwszej sprzedaży doszedł do wniosku, że oferując 0,25 $ za każdy bloczek będzie mógł kupić tyle bloczków ile zechce. Później mógłby je sprzedać w swoim sklepie po 0,5 $ za jeden. Natomiast oferta 4 $ za każdą deskę (deski później może sprzedać po 5 $ za jedną) zapewni mu zakup ich w takiej ilości jakiej zapragnie. Jednym ograniczeniem kupna wspomnianych materiałów jest pojemność samochodu dostawczego. Nie może on załadować więcej niż 2 tony towaru oraz 60 cubic feet (cubic feet jest to miara objętości odpowiadająca wymiarom kostki o krawędziach 0,30 cra*0,30cm*0,30cm). Każdy bloczek waży 36,32 kg i ma 0,5 cubic foot. Każda deska waży 18,16 kg i ma 1 cubic foot objętości. Jaką ilość bloczków i desek powinien nabyć na aukcji Joe Carpenter, aby osiągnął maksymalny zysk ze sprzedaży? Zakładamy, że Joe może wykonać tylko jeden przejazd swoim samochodem, a) Rozwiąż problem stosując metodę graficzną.

b)    Określ optymalny zakres dla jednostkowego zysku z bloczków betonowych.

c)    Wyznacz cenę dualną związaną z limitem objętości załadunku i jej zakres stosowalności.

Rozwiązanie.

a) = 0, x₂ = 60,    = 60. b) c, e 0,5].

e) Cena dualna wynosi l,ajej zakres stosowalności RHS₂ e (0; 110,1322].

2, Mając dany model matematyczny i rozwiązanie pewnego problemu (alokacji środków produkcji), wyznacz zakresy optymalne oraz ceny dualne i ich zakresy stosowalności.

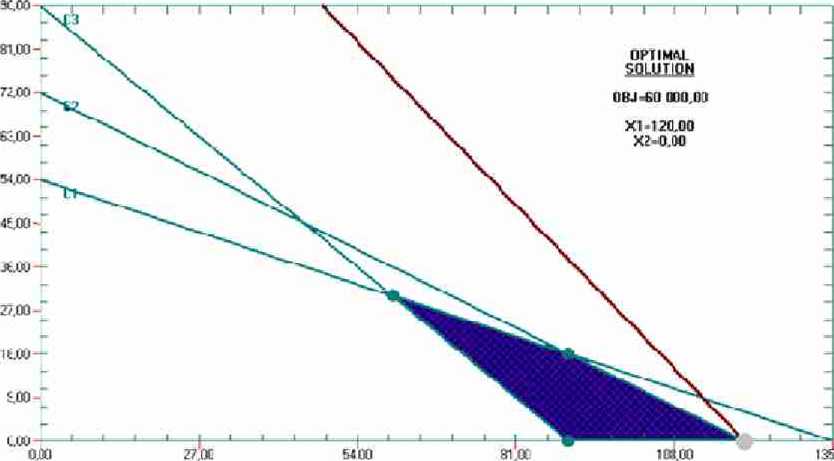
135.01

500*j + 400*2 max

2*j +5*2 ^ 270 3*] +5*2 ź 360

*j + *2 2:90

*j,*2 £0