1300739572

Wprowadzenie do podstaw automatyki

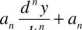
d"~'y    d"~²y

dt'

dt" ¹ dt'

+ ... + a₀y =

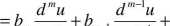
dt"'

n>m (1.1)

gdzie: y - sygnał wyjściowy, u - sygnał wejściowy, a_t i bj - stałe współczynniki równania różniczkowego (0 <i<n, 0 < j <m)

Dla wszystkich układów rzeczywistych wszystkie elementy rzeczywiste mają charakter inercyjny, stąd n>m.

Równanie charakterystyki statycznej (wszystkie pochodne funkcji wejścia i wyjścia są zerowe) wynikające z równania różniczkowego (1.1) ma postać

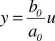
(1.2)

Charakterystyka statyczna układu liniowego lub zlinearyzowanego w otoczeniu nominalnego punktu pracy (u,y są odchyłkami od tego punktu) ma postać:

u

Rysunek 1.5. Charakterystyka statyczna

Początek układu współrzędnych oznacza nominalny punkt pracy, a sygnały wejścia u i wyjścia y są odchyłkami sygnałów od tego punktu.

Aby ocenić właściwości dynamiczne na podstawie przebiegów przejściowych (nieustalonych) należy rozwiązać równanie (1.1). Po rozwiązaniu otrzymamy odpowiedź na wyjściu y(t) na zadany sygnał na wejściu u(t). Najczęściej jest to skok jednostkowy u(t) = l(t).

Strona 17