2740389303

to prawdopodobieństwo zdarzenia B_n polegającego na otrzymaniu kuli białej w n-tym

losowaniu jest równe - dla każdego n. Stąd wynika, że dla każdych n,m prawdziwa b + c

jest równość P(B_n I B_m) = P(B_m I B_n).

Zadanie 7.

W pojemniku jest dziesięć monet. Siedem jest prawidłowych, a trzy mają orły po obu stronach. Losowo wybraną monetą rzucono pięć razy i otrzymano pięć razy orła. Oblicz prawdopodobieństwo, że rzucano monetą z orłami po obu stronach.

Szkic rozwiązania

Wprowadźmy oznaczenia dla zdarzeń:

H, - wylosujemy monetę z orłami po obu stronach,

H, - wylosujemy monetę prawidłową,

A - otrzymamy pięć razy orła.

Mamy obliczyć prawdopodobieństwo warunkowe P(H, I A).

p₍H _|A)_P(AnH,) P( Al H,)P(H,)

'    P(A)    P( A)

Zdarzenia H,,H, spełniają założenia twierdzenia o prawdopodobieństwie całkowitym.

3    7    11

H, uH, = Q,H, nH, = 0,P(H,) = —, P(H,) = —, P(AIH.) = 1, P(AIH,) = — = — .

'    ^{2    1    2    1}    10    ²    10    ^1    2    2    32

Zdarzenia H,,H, spełniają założenia twierdzenia o prawdopodobieństwie całkowitym.

P(A) = P(AIH,)P(H₁) + P(AIH₂)P(H₂).

Stąd

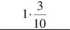
¹ 10⁺32 10

96

103'

Zadanie 8.

Na półce stoją dwa pojemniki. W pierwszym pojemniku jest pięć kul: cztery białe i jedna czarna, a drugim są trzy kule: dwie białe i jedna czarna. Z losowo wybranego pojemnika wybieramy losowo dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo warunkowe, że druga wylosowana kula będzie biała, jeżeli wiadomo, że pierwsza wylosowana kula była biała.

Szkic rozwiązania

Wprowadźmy oznaczenia dla zdarzeń:

H, - wylosujemy pierwszy pojemnik,

H, - wylosujemy drugi pojemnik,

B, - pierwsza wylosowana kula będzie biała,

B, - druga wylosowana kula będzie biała.

14