3226794664

4. PRAWDOPODOBIEŃSTWO WARUNKOWE

P(A\B) - prawdopodobieństwo warunkowe zajścia zdarzenia A pod warunkiem zajścia zd. B

P(A O B)

P(A|B) =

P(B)

dla

( P(B) >0 A A,Bcft )

Wniosek: Jeżeli A, B cz fi oraz P(B)>0, to P(A n B) = P(A | B) • P(B)

5. PRAWDOPODOBIEŃSTWO CAŁKOWITE (ZUPEŁNE)

Jeżeli zdarzenia: Bi, B2.....B„ a Cl tworzą zupełny układ zdarzeń (hipotez), izn. spełniają warunki:

1) B, n B_y = 0 dla ij e { 1,2,3, * n} a i j (zdarzenia wykluczają się parami),

2) B, u B₂ u B3 u ... u B„ = kl    (suma wszystkich zdarz.eń jest zdarzeniem pewnym Ii),

3)    P(Bj) > 0    dla 1'e { 1.2,3,...,/?)    (ich prawdopodobieństwa są dodatnie).

to dla każdego A c H zachodzi poniższy wzór na prawdopodobieństwo całkowite (zupełne)

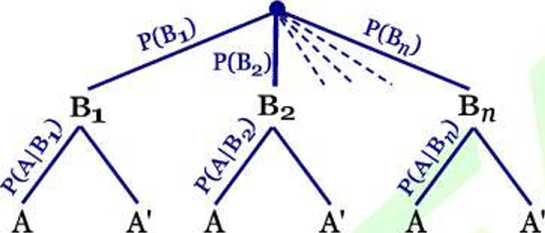
P(B_fc|A) =

P(A) = PCAIBJ • P(B_Jl) + P(A|B_Z) •

P(B₂) + ... + P(A|B„) • P(B_n)

analogicznie otrzymamy wzjór:

P(A) = P(A O Bi) + P(A O B_z) +

+ .., + p(An B„)

Jeżeli znamy wynik doświadczenia i pytamy jedynie o jego przebieg, to stosujemy poniższy wzór (twierdzenie) Bayesa:

A P(B) > 0

_P(AlBfc) • P(Bfc)_

P(A|B!) • P(fc) + P(A|B₂) • P(B₂) + ... + P(A|B„) • P(B„)

6. ZDARZENIA NIEZALEŻNE

P(A n B) = P(A) - P(B)    [P(B) = 0 lub P(A|B) = P(A)aP(B)>0]

analogicznie:    P(A n A, n A₂ n ... n A_n) = P(A) ■ P(A₍) ■ P(A2>"... ■ P(A_n)

Za niezależne uznajemy doświadczenia polegające na losowaniu ze zwracaniem, losowaniu ze zbiorów rozłącznych oraz na oddawaniu kilku strzałów przez jednego lub kilku strzelców.

7. SCHEMAT BERNOULLIEGO

Próby niezależne - wynik każdego z ciągu kilku doświadczeń losowych nie zależy od wyników pozostałych.

Niezależne próby nazywamy próbami Bernoulliego. jeśli spełnione są następujące warunki:

-    każda próba może zakończyć się jednym z dwóch wyników: A - sukces. A' -porażka

-    prawdopodobieństwo sukcesu w każdej próbie jest takie samo.

Prawdopodobieństwo wypadnięcia w n niezależnych próbach Bernoulliego dokładnie k sukcesów:

Schemat Bernoulliego:    P ({S_n = fc}) = P„(fc) =    ■ Cf^{n h}

gdzie: p - prawdopodobieństwo sukcesu (0 < p < 1) w pojedynczej próbie Bernoulliego q - prawdopodobieństwo porażki (q = 1 — p) w jednej próbie Bernoulliego k - ilość sukcesów ( 0 < k - S„ <n) w n próbach Bernoulliego P_n(k) - prawdopodobieństwo uzyskania k sukcesów w n próbach Bernoulliego ko - najbardziej prawdopodobna liczba sukcesów w // próbach dla P(S„=ko) > P(.S'„=A').

L.p.	Próby Bernoulliego	Sukces	Porażka
I.	rzut monetą	orzeł	reszka
2.	rz.ut kością	co najmniej 3 oczka	1 lub 2 oczka
3.	strzelanie tlo celu	trafienie	nie trafienie

-328-

w w w. ma tematyka. sosu o wiec.p l

© Copyright by Ewa Kędziorczyk