4544139882

14 Zbiór zadań z rachunku prawdopodobieństwa i statystyki matematycznej

108. Niech

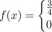
| (1 - I²) dla — 1 < x < 1,

poza tym.

P(X<-i), P(|X|>1).

Narysować wykres /, znaleźć dystrybuantę i narysować jej wykres, obliczyć EX, D²X,

109. Dobrać tak stalą a, by funkcja

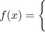
a- cosx dla — ^ < x < 0    poza tym

była gęstością pewnej zmiennej losowej X. Narysować wykres /, znaleźć dystrybuantę i narysować jej wykres, obliczyć EX, D²X, P(\X\ > |), P(X > ^),P(—| < X < |) oraz medianę i modę X.

110. Funkcja gęstości prawdopodobieństwa zmiennej losowej X jest postaci:

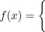
0    dla x ^ 0

2e^-2x dla a; > 0.

Narysować wykres /, znaleźć dystrybuantę i narysować jej wykres, obliczyć EX, D²X, P(X > 1), P(0 < X < ln 3) oraz medianę X.

111. Niech gęstość pewnej zmiennej X będzie postaci

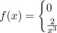
dla x < 1, dla x > 1.

Narysować wykres /, znaleźć dystrybuantę i narysować jej wykres, obliczyć EX, D²X, P(|X| > 1) oraz medianę X.

112.    Niech f(x) = ^    dla x € M. Narysować wykres /, znaleźć dystrybuantę i narysować jej wykres, zbadać istnienie EX. Obliczyć P(0 < X < 1), P(SX — 1 >    — 1),

P(0 < X < \/3). Znaleźć medianę oraz modę.

113.    Zmienna X ma gęstość postaci

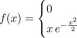
dla x < 0, dla x > 0.

Znaleźć dystrybuantę, medianę, modę, wartość oczekiwaną, P(X > \/ki 4), P(X < \/ln 9).

114. Zmienna X ma gęstość postaci

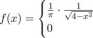
dla |x| < 2,

poza tym.

Zbadać istnienie EX. Wyznaczyć dystrybuantę X oraz obliczyć P(1 < X < 2).

115. Zmienna X ma gęstość postaci

/m =

e^2x dla x £ (0, ln^), 0 poza tym.

Znaleźć P(ln2 < X < 1), P(X < ln^).

@ Copyright by W. Młocek, K. Piwowarczyk and A. Rutkowska