17127

Usta 1

Działania na wektorach

1.    Dane są dwa wektory: a = 3i +4j -5koraz b = -i + 2j + 6k. Wyznaczyć (a) długość każdego wektora, (b) iloczyn skalarny ab, (c) kąt pomiędzy wektorami (a - b) oraz (a + b).

2.    (*) Wektory a i b spełniają relacje: a + b = 1 li - j + 5k , a - fb = -25i+ 17j- 6k Wyznaczyć wektory a i b . Czy wektory te są do siebie równoległe lub prostopadłe?

3.    Dany jest wektor a = 6i + 4j .Wyznaczyć wektor jednostkowy prostopadły do wektora a.

4.    (*) Dane są dwa wektory a = 3i+4joraz b = 6i + 16j. Rozłożyć wektor b na składową równoległą do wektora a oraz do niego prostopadłą.

5.    W punktach o współrzędnych (2,2) oraz ( 3,7) kartezjańskiego wkładu współrzędnych umieszczono po jednej cząstce. Wyznaczyć kąt jaki tworzą wektory wodzące cząstek z osią OX.

6.    W kartezjańskim układzie współrzędnych dane są dwa punkty M!(2,10) oraz M₂(5,6). Jaki kąt z osią OX tworzy prosta łącząca oba punkty ?

7.    Wektory a oraz b spełniają relacje: a + b = 0. Co możemy powiedzieć o tych wektorach ?

8.    (*) Poruszająca się po podłodze z prędkością o wartości V| kula uderza w ścianę pod kątem a i odbija się pod kątem p. Nowa wartość prędkości wynosi V2. Wyznaczyć wektor zmiany prędkości.

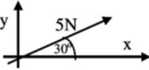
9.    (*) Przedstawić wektor z rysunku jako sumę dwu wektorów:

jednego w kierunku osi OX i drugiego w kierunku osi OY.

Wprowadzić wektory jednostkowe i oraz j. Zapisać wektor w postaci A= \i + Ay j tzn. rozłożyć wektor na składowe.

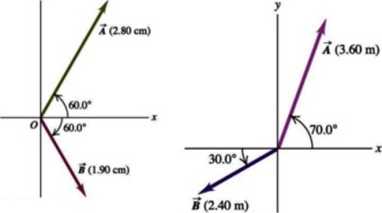
10. (*) Przedstawić każdy z wektorów z poniższego rysunku jako sumę dwu wektorów: jednego w kierunku osi OX i drugiego w kierunku osi OY. Wprowadzić wektory jednostkowe i oraz j. Zapisać każdy z wektorów w postaci A= A*i + Ay j.

y