23371

Twierdzenie o wartości średnie] (twierdzenie Lagrangea)

/(!>)-f (a) b-a

/€ c(M)|

/€ D((a.b))J

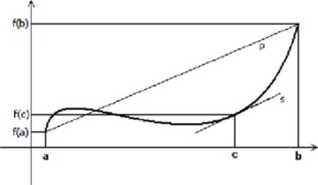
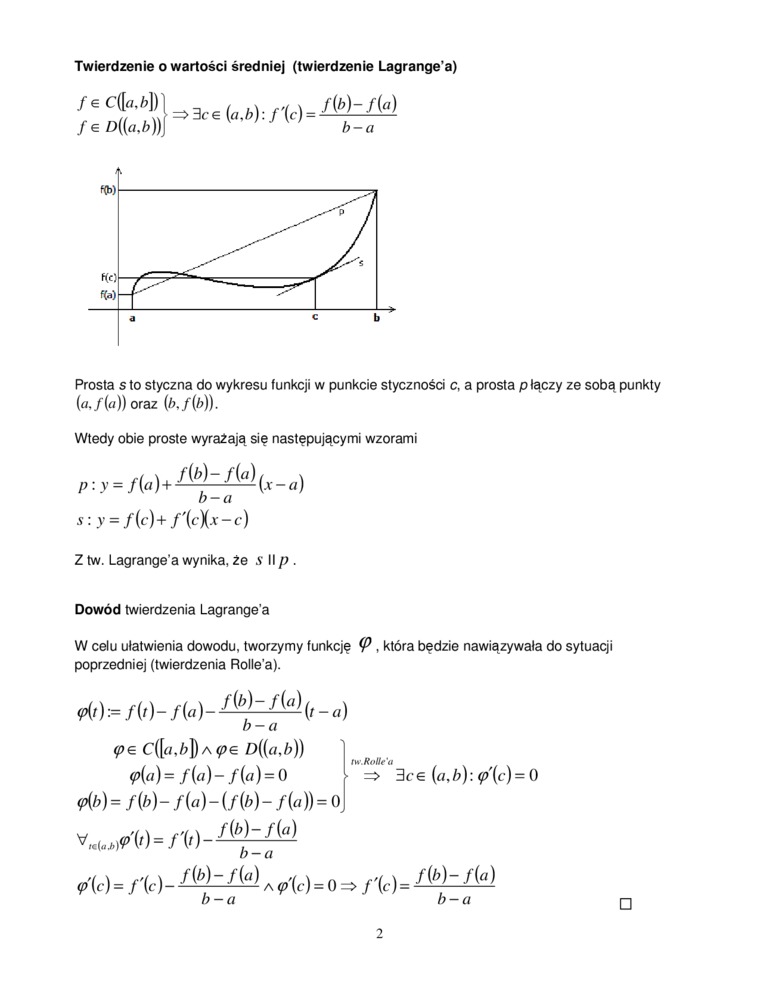
Prosta s to styczna do wykresu funkcji w punkcie styczności c, a prosta p łączy ze sobą punkty (*./(<»)) oraz (bj(b)).

b-a

s:y = f(c)+f'(c'j(x-c)

Wtedy obie proste wyrażają się następującymi wzorami P'

Z tw. Lagrange'a wynika, że s W p .

Dowód twierdzenia Lagrange'a

W celu ułatwienia dowodu, tworzymy funkcję <P , która będzie nawiązywała do sytuacji poprzedniej (twierdzenia Rolle'a).

b-a

<pe C([a,b])A<pe D((a_yb))    ]

tw.KotteUt

^(«)=/(«)-/(") = 0    \ => 3ce(a,b):<p'(c)=0

<p(b)= f(b)~ f(a)-(f(b)-f(a)) = oj

f>’M • rW-ĄzZfc) _A o =. /•«, IfehlW

b-a    b-a

2