0099

101

§ 2. Własności całek oznaczonych

306. Drugie twierdzenie o wartości średniej. Udowodnimy tu jeszcze jedno twierdzenie o całce z iloczynu dwóch funkcji

I = f'f(x)g(x)dx.

a

Jest ono podawane w rozmaitych postaciach. Zaczniemy od dowodu następującego twierdzenia:

13° Jeśli w przedziale <a, by (a < b) funkcja f{x) jest monofonicznie malejąca (choćby w szerszym sensie) i nieujemna, a funkcja g{x) jest całkowalna, to

b    s

(3)    J f(x) g (x) dx = f(a) J g (x) dx ,

a    a

gdzie f oznacza pewną liczbę z rozpatrywanego przedziału.

Rozbijając przedział {a, b) w dowolny sposób na podprzedziały za pomocą punktów podziału x, (/ = 0, 1, ..., n), przedstawiamy całkę I w postaci

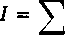
)’ /(*) g (x) dx = jr/(x,) J g (x) dx+ ^ j [/(x)-/(x,)] g (x) dx = o+p.

i    1=0    X1    1=0 X,

Jeśli przez L oznaczymy kres górny funkcji \g (x)|, a przez to_f (jak zwykle) oscylację funkcji/(x) w /-tym podprzedziale (x_j( x,+₁) o długości Ax_t, to oczywiście mamy

u— 1 xi + i    u—1

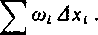
lp| < ^ f lf(x)-f(x,)l Ig (x)| dx < L

i-0 x,    i-0

Wobec tego z całkowalności funkcji f(x) [298, 111] wynika, że p -* 0, jeśli A = = max zlX(-»0, zatem

I = lim a .

A-O

Wprowadzamy teraz funkcję

G (x) = J g (/) dt

i za pomocą tej funkcji przedstawimy sumę a w postaci

<T

Y/(*,) [G (x i + l)^— G (X|)]

i-o

i wreszcie, po otwarciu nawiasów i zgrupowaniu odpowiednio składników, w postaci

<r = |]G(X|) [/(x_i-₁)—/(x,)] + G (ó)/(x„_i).

1-1

Jeśli zmienna x przebiega przedział <o, by, to funkcja ciągła G (x) [305, 11°] przyjmuje zarówno swą wartość najmniejszą m, jak i wartość największą M [85]. Ponieważ wszystkie czynniki

f(Xi-i)-f(xj) (dla i = 1,2.....n-1) i f(x_n-_l)