0101

§ 2. Własności całek oznaczonych

103

W szczególności

(5*)

J/(*) 9 (*) dx = /(a+0) J g (x) dx+f(b-0) j g (x) dx ,

Przez | oznaczamy tu, podobnie jak poprzednio, pewną liczbę z przedziału <a, 6>, jednakże zależy ona na ogól od wyboru liczb A i B.

§ 3. Obliczanie i przekształcanie całek oznaczonych

307. Obliczanie za pomocą sum całkowych. Podamy kilka przykładów obliczania całki oznaczonej bezpośrednio jako granicy sum całkowych — zgodnie z definicją. Wiedząc z góry, że całka funkcji ciągłej zawsze istnieje, do obliczania jej możemy tak wybierać podziały przedziału i punkty £,, jak nam jest najwygodniej.

b

1) fx^kdx (a, b — dowolne liczby rzeczywiste, k — liczba naturalna).

0

Najpierw znajdziemy całkę jx^kdx (a=^0). Przedział <0, a> podzielimy na n równych części, a w każ-o

dym podprzedziaJe obliczymy wartość funkcji x* w prawym jego końcu, jeśli a>0, a w lewym, jeśli a<0. Wtedy suma całkowa jest równa

= a*⁴¹-

l*+2*+ ...-f/i*

czyli, uwzględniając przykład 14) z ustępu 33,

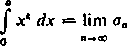
a*⁴' k+1 '

Stąd łatwo już otrzymuje się wzór ogólny

b    ba

}'x*dx = /- /

0 0 0

AH-l

b

2) fx*dx (b> a>0,    — dowolna liczba rzeczywista).

a

Tym razem przedział <a, ó> rozbijemy na nierówne części, a mianowicie między a i b wstawiamy n— 1 średnich geometrycznych. Innymi słowy biorąc

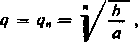
rozpatrzymy ciąg liczb

a, ag, .... aq‘, ..., ag" = b.

Zauważmy, że gdy n-* oo iloraz $ = r/„-*-l, natomiast różnica — ag¹ jest zawsze mniejsza od wielkości b (q„ -1 )-»-0.