0115

§ 3. Obliczanie i przekształcanie całek oznaczonych

117

czyli

/

x sin x 1-j-cos²*

dx

/

sin / l-fcos²r

dt-

I

t sin t l+cos²f

dt.

Przenosząc ostatnią całkę (w której zastępujemy literę t z powrotem przez ,v) na lewą stronę tej równości i dzieląc ją stronami przez 2, otrzymujemy

J

x sin x 1-1-cos²*

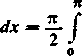
sin t 14-cos²/

dt

•2- arc tg (cos t)

4

Porównaj dalej 11), gdzie przykład ten zostanie uogólniony.

1

5) obliczyć całkę J — f    dx.

J 1 “T X O

Podstawienie * = tg ę> (gdzie <p zmienia się od 0 do n) prowadzi do całki

J In (1 -(-tg <p) d<p .

o

Ale

l + tgę>

yT sin

cos <p

a więc

«/4

./=-i-7t In 2+J ln sin    / Ir\ cos q>d<p.

o    o

Ponieważ obie ostatnie całki są równe (drugą całkę można sprowadzić do poprzedzającej ją przez podstawienie <p =— n—y>, przy czym y> zmienia się od —n do 0), więc ostatecznie

/ = -i- 7t ln 2 .

Zauważmy, że taką samą wartość ma całka

i

fąrctgx_j J l+x

l+x

U

o czym łatwo można się przekonać, całkując ją przez części. 6) Udowodnić, że

1    7C/2

[*££*.dx-± f ——dt. •' x    2 J sin t

Wskazówka. Wykonać podstawienie x = tgy t. 7) Udowodnić równość

rr    n

f (x+ y/x²—1 cos <p)ⁿd<p — f '    —-

~    j (x— y'*²—1 cos 0)""^1-1

przy założeniu, że n jest liczbą naturalną i że x> 1.