0107

109

§ -3. Obliczanie i przekształcanie całek oznaczonych

nika z wniosku w ustępie 131, wystarczy założyć to tylko dla przedziału otwartego (a, b), jeśli tylko funkcja F(x) jest ciągła w końcach tego przedziału.

Dlatego też mamy na przykład prawo napisać [268]

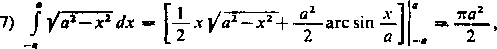
chociaż dla x — ±a sprawa istnienia pochodnej znalezionej funkcji pierwotnej wymagałaby jeszcze zbadania.

Pewne trudności napotykamy przy obliczaniu całki:

8) f --

J 1-2 r

-dx (0 < r < 1) ,

1—r²

■ COS X+r²

-Tt

ponieważ obliczona w ustępie 288, 13) funkcja pierwotna

F(x) = 2 arc tg ^ |tg y j

nie ma sensu dla x = ±tt. Jednakże istnieją oczywiście granice

lim F(jr)==—7t,    lim F(x)=rc,

x-*—TC+O    X-.Tt-0

i jeśli przyjmiemy, jak zwykle, że wartości funkcji F(—n) i F(n) są odpowiednio równe tym granicom, to funkcja F(x) jest nie tylko określona, ale nawet ciągła w końcach przedziału. Dlatego też mamy

J-

1 —r²

dx = F(x)

2r cos x+r²

—75

9) W analogiczny sposób obliczamy całkę

7C/2

/

-«/a

dx

= F(n)-.F(-n) = 2n.

A cos²ar+2B cos x sin x+C sin²*

(AC-B² > 0).

Znamy już [288, 10)] funkcję pierwotną F W =

—^-aretgJpM^gr

]/AC-B²    yAC-B²

funkcji podcałkowej w przedziale otwartym (—tu/2, 7t/2). A więc */2

I

-n/a

dx

A cos²*+2.Bcos x sin x+ D sin²*

= FW

n/a-o

-n/a+o    yAD—B²

przy tym znaki —-i-n+0,-^7t—0 wskazują na konieczność wzięcia odpowiednich wartości granicznych funkcji F(x).

10) Jeśli przy obliczaniu całki

/

*⁴+l

*⁶+l

dx