0103

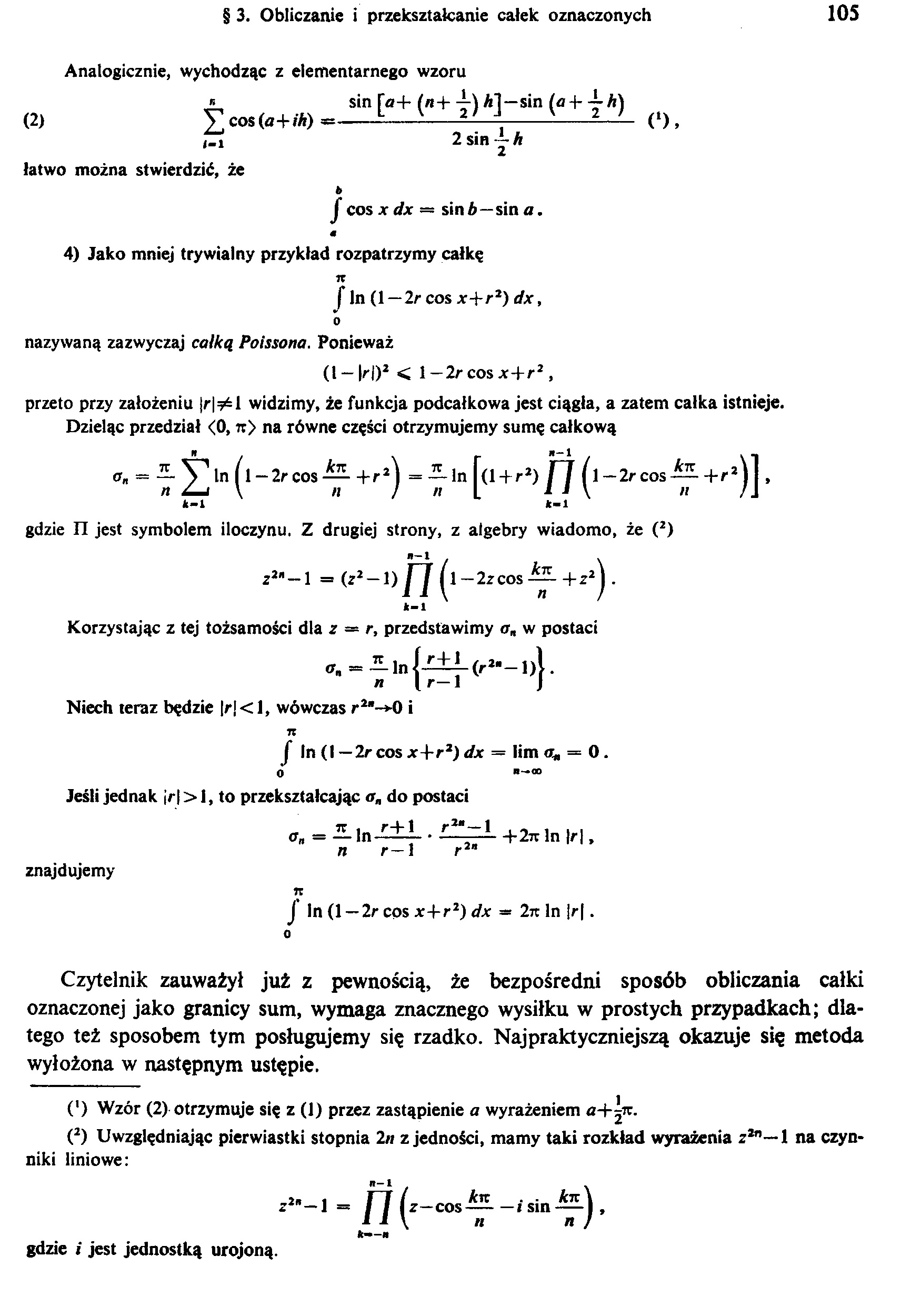
(2)

(2)

105

§ 3. Obliczanie i przekształcanie całek oznaczonych

Analogicznie, wychodząc z elementarnego wzoru

E^cos

i-i

łatwo można stwierdzić, że

sin fa+ (n+    Al—sin laĄ- -i-A)

2 sin — h z

(«+/*) -^L-—i-²—.-i-O,

j cos x dx — sin b—sin a.

m

4) Jako mniej trywialny przykład rozpatrzymy całkę

TT

f ln (1—2r cos x+r²) dx,

nazywaną zazwyczaj całką Poissona. Ponieważ

(l — H)² < 1—2rcosJt+r²,

przeto przy założeniu |r|#l widzimy, że funkcja podcałkowa jest ciągła, a zatem całka istnieje. Dzieląc przedział <0, ir> na równe części otrzymujemy sumę całkową

a„ = i^ln^l-2rcos-^-+r²j = ^-ln|u + r²) j~] ^l-2rcos-^+r²jj ,

W-l

tt \ ^ .    (.    -    len «\ n .    \ ..

On

n

k-l    "    km 1

gdzie II jest symbolem iloczynu. Z drugiej strony, z algebry wiadomo, że (²)

m.

1 —2rcos    +z² j .

Korzystając z tej tożsamości dla z — r, przedstawimy <x„ w postaci Niech teraz będzie |r|<l, wówczas r²"->0 i

n

J In (I —2r cos x+r²) dx = lim <7* = 0.

_a„ ₌ JL_lnl±L.Ć^L₊₂nln\r\,

n r—1 r^2a

Jeśli jednak ir| > 1, to przekształcając <r„ do postaci znajdujemy

J In (1 — 2r cos x+r²) dx = 27t ln |r|.

Czytelnik zauważył już z pewnością, że bezpośredni sposób obliczania całki oznaczonej jako granicy sum, wymaga znacznego wysiłku w prostych przypadkach; dlatego też sposobem tym posługujemy się rzadko. Najpraktyczniejszą okazuje się metoda wyłożona w następnym ustępie.

0) Wzór (2) otrzymuje się z (1) przez zastąpienie a wyrażeniem a+^K.

(²) Uwzględniając pierwiastki stopnia 2/i z jedności, mamy taki rozkład wyłażenia z^In— 1 na czynniki liniowe:

f)-

kit . ■ kit

cos--1 sin

tt

gdzie i jest jednostką urojoną.