005

XI. ZASTOSOWANIE CAŁEK OZNACZONYCH

A. POLE FIGURY PŁASKIEJ

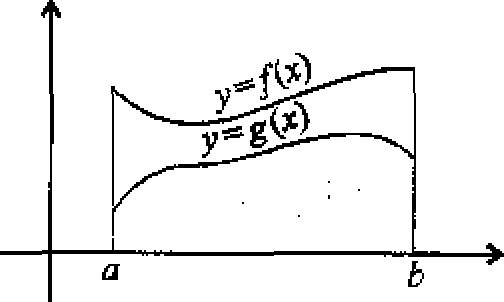
Zastosowanie wzoru na obliczanie pola trapezu krzywoliniowego (wynikającego z definicji całki oznaczonej, zob* początek Rozdziału X) można rozszerzyć w następujący sposób. Rozważmy krzywe y = f(x) oraz y = g(x) dla x € [a, 6], takie iż na tym odcinku zawsze /(:/;) > g{x) oraz, że te funkcje są tu ciągle. Pole obszaru między tymi krzywymi oraz prostymi x = a oraz x = 6 wyraża się wzorem w pierwszej ramce u dołu strony. Wzór ten jest oczywisty w prostszej sytuacji, gdy dodatkowo założymy, iż g(x) >0 dla a < x < h. Wystarczy odjąć pola trapezów krzywoliniowych jak na rysunku obok i zastosować Własność 1 z Rozdziału X,

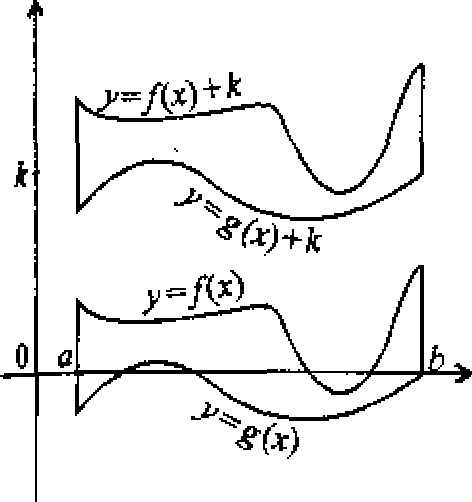
Rozważmy teraz ogólną sytuację, gdy to dodatkowe założenie nie zachodzi. Przesuńmy pionowo w górę obie krzywe i figurę zawartą między nimi na tyle wysoko, aby przesunięta figura leżała całkowicie nad osią Ox. Powiedzmy, że należy dokonać przesunięcia o k jednostek. Przesunięte krzywe mają więc równania y = f(x)-\-k oraz y = g{x) + A:. Pole figury nie ulega zmianie przy prze-

h

sunięciu. Wynosi ono więc J [(/(— (#(tf)-hfc)] dx =

a

b    b

J[f(x) - g(x) + k - k]dx = f[f(x) - g(x)J dx, co należało

n    a

wykazać.

Oto wzory na pole figury płaskiej we współrzędnych kartę zj ans kich, biegunowych i parametrycznych.

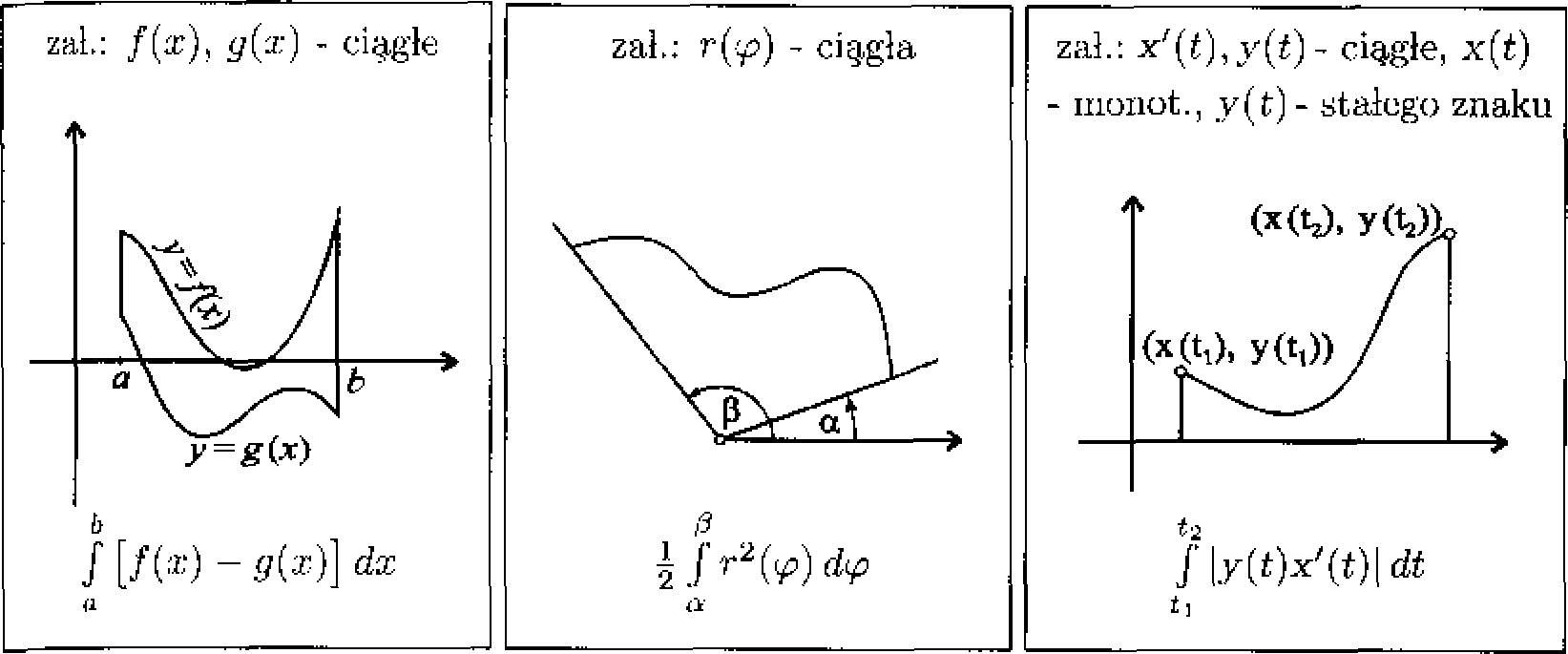
89