DSC07148 (5)

224

Zastosowanie całek oznaczonych

c) Ponieważ /(*) — arcsin (f *), zatem /*(i) = —y?    —r— Długość krzywej wyraża

.___ v 1 —

sug wzorem    - ₍_

in

^{=    =} t^,n (^u+ v^/=riT) I! = ^ta (^e+

⁰    i

d)    Ponieważ /*(*) = —, więc szukana długość luku krzywej dana jest wzorem

in

Jv9 | Ji/a    2^2

^p~

V5    yS    ,/J

dr.

V5    V5

Jeżeli teraz w całce ^ ———— di dokonamy podstawienia x = sh t, to otrzymamy

■- l + Vx² + l _+c

/

n/x^j + 1

dz = yz^-ł-l — ln

Zatem

3v/5

✓5

|'^p - [v#lT-i«|łteS±I!

= 3-ln>/2-(2-lnv/3) = l+lnv^/3-lnv/2 = l+biyJĘ.

• Przykład 9.3

a)    Podstawą bryły jest koło o promieniu R. Każdy przekrój bryły płaszczyzną prostopadłą do ustalonej średnicy koła jest trójkątem równobocznym. Obliczyć objętość tej bryły.

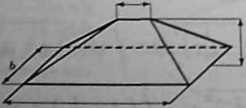
b)    Wyprowadzić wzór na objętość pryzmy o wymiarach podanych na rysunku.

h

c*) Obliczyć objętość bryły ograniczonej powierzchniami:

|f + § - &, z³ + z^a = IP.

Przykłady

Rozwiązanie

W rozwiązaniach wykorzystamy wzór

k

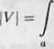
S(x) dx,

w którym S(x) oznacza pole przekroju bryły płaszczyzną prostopadłą do ustalonej osi. a) Ze względu na symetrię bryły względem płaszczyzn z = 0, y = 0 wystarczy obliczyć objętość jej ćwiartki (rysunek).

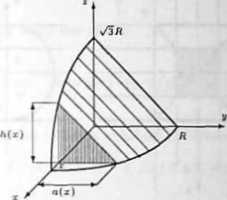
Korzystając z danych zadania wyznaczymy pole przekroju S(z). Mamy

S(x) = \a(x)h{x) = \s/R'-x'-y/3-y/R? -x* = ^(fl*-r^a). gdzie 0 $ x $ R. Zatem

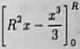
*    ^R    i W

J S(x)dx = ^ J (R⁷-x²)dx=^

a    0

Ostatecznie objętość rozważanej bryły jest równa —r—R*.

V

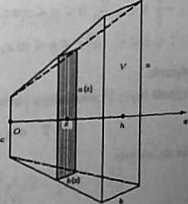
b) Niech osią Oz będzie prosta prostopadła dó podstawy, a jej początek niech będzie na krawędzi c (rysunek). Przekrój pryzmy płaszczyzną prostopadłą do osi Ox jest prostokątem. Długości boków tego prostokąta oznaczamy przez a(x) i 6(z). Z podobieństwa odpowiednich trójkątów wynika, że wyrażają się one wzorami:

a(x) = c+ ^(a — c), 6(z) = c + ^6, gdzie 0 ś x $ 6. Zatem

a \    < ...» » bchx + 6(a - ć)x^a

S(z) = o(z)6(z) --^