DSC07149 (6)

226

Zastosowanie całek oznaczonych

Stąd

= JS(x)dx= jrj J (cóx+(a-c)x^a) dx = p-

chx³ (a—c)x^ł 2 ⁺    3

i 6h(c+2a)

6 i

c») Bryła P rozważana w zadaniu jest ograniczona dwiema powierzchniami walcowymi. 2 R

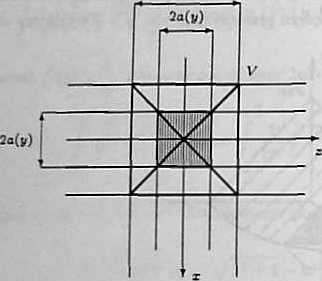
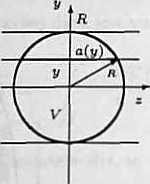
Na pierwszym rysunku przedstawiony jest widok tęj bryły z kierunku osi Oy, a na drugim pokazany jest przekrój bryły płaszczyzną równoległą do płaszczyzny xOz i przecinającą oś Oy w punkcie y. gdzie —R $ y $ R. Przekrój ten jest kwadratem o boku 2a(y), gdzie a(y) = y/R? — y³. Ze wzglądu na symetrią bryły V wzglądem płaszczyzn układu mamy

|V|

« «

= 8 Ja²{y)dy = 8 J (*^a-y²) dy = 8

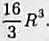
■ Przykład 9.4

Obliczyć objętości brył powstałych z obrotu podanych figur T wokół wskazanych od:

a)T: ~<x<~,0<v<cobx,Ox; b)T:0<x<l, 0 < y < e"^B, Oy; c) T: 1 < x < e, ln² x < y < łnx, Ox; d) T: 0 < x < 1, X² < y < >/*, Oy. Rozwiązanie

a) Objętość bryły V powstałej z obrotu wokół osi Ox obszaru

T:aśxśb, Ośyt;/(x),

wyrażaną wzorem

Przykłady

Objętość rozważanej bryły jest równa

i    *

|V| = JT J cos³ x di = JT + ^siniej* = 1*’.

-f

b)    Objętość bryły V powstałej z obrotu obszaru T: 0 $ o $ i ^ 6,    J(x) wokół

oś Oy wyraża się wzorem:

k

|V| = 2>r J xf(x)dx.

a

Zatem objętość rozważanej bryły jest równa i

\V\ = 2ir jxe~^xdx=2ir [—(a: + l)e^-*]„ = 2ir (l -1).

0

c)    Objętość bryły V powstałej z obrotu wokół osi 0x obszaru

T : a ^ 1^6, 0$ /(z) $ y $ g(z)

wyraża się wzorem

b

\v\ = *j [g\x)-f\x)]dr.

'a'-' ■

Ponieważ dla obszaru T rozważanego w zadaniu mamy o = 1, 6 = e, /(z) = ln^łx, g(x) = ln z, więc

e

|V| = 7r J (ln x — ln³ z) dx

= ff^(złnz —z) — (xln³z-2xlnx + 2z) j = ir(3- e).

d) Objętość bryły V powstałej z obrotu figury

T: 0$a$z$6, /(x) i? y $ g(x), wokół osi Oy, wyraża się wzorem

HO

|V|=2ff Jz[y(x) - /(*)].dx.

O

Zatem    ^

IMI = 2»r Jx (y/Z - z³) dx = 2tt ._v0 . :