DSC07147 (6)

222

Zastosowanie całek oznaczonych

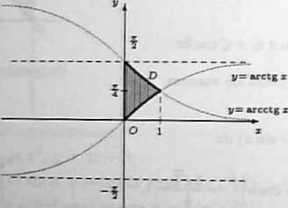
d) Rozważony obszar D można opisać przez nierówności:

tylko dolnej części tego obszaru. Mamy zatem

ł

\D\ = 2 / tgy<ły = -2[ln|cosy|]^T = ln2.

l$y$\/e. -lny    giny.

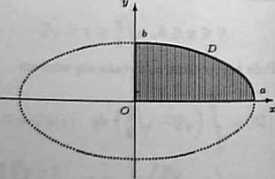
f) Z symetrii elipsy

a*

1

£

P

względem obu on wynika, że wystarczy ob-pole ograniczone osią Oz, osią Oy oraz lukiem elipsy y = iy/tf - x?, gdzie 0 < z < o, i otrqrmany°wynik pomnożyć pnez 4. Zatem Brukane pole dane jest wzo-BBK

\D\ =

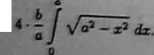
Przykłady

Wykorzystując podstawienie z = orani w calce nieoznaczonej otrzymamy f y/a² —x² <łx = 7; \/a^J — z^J + aresin - + C.

J    2    56’.- ' ■    ‘ O'. ’

Tak więc

„J

223

j y/a²-x² dx= j|v/a¹-z* + y

. x arcsin — a

a , 2 na* = y arcsin 1 = —

Pole elipsy wyraża się zatem wzorem

|D| = 4 ■ - •    = nab.

a 4

Przykład 9.2

Obliczyć długości łuków podanych krzywych:

^a) V = V1 - x-< gdzie x G

i

z⁴ 1

^{b)l/ =} T⁺8?’^edziea:el^1,3'^;

c) y = arcsin (e^_I), gdzie x G [0,1]; d) y = lni, gdzie z G [\Z3,2\/2]. Rozwiązanie

Długość krzywej T : y = /(z), gdzie z 6 [a,6j, wyraża się wzorem

in

ł> _

= J ^/l + l/'(*)|^łdz.

a) Dla funkcji /(z) = \/l - z³ mamy /'(z) = -7—=_=. Zatem

VI-s®

|T|

-J^J¹⁺ G/S*)

b) Dla funkcji /(z) =    mamy /'(z) = z³ — Zatem

4*3

PI

= / )/¹+(*^,-5r) ^tfa=/y*‘⁺5 ⁺ IS?*

¹    3    ¹

= |    ^dr=/(^iS+4?)^ar={^"^].

I X 1*181 9 '