0129

§ 4. Niektóre zastosowania całek oznaczonych

131

przedział ten na podprzedziały o długościach Ax, = x_l+i—x,. Podstawmy teraz w nierówności (12) Pi = p (a'i) Axi, a, = ip (xi). Otrzymujemy nierówność

V p(x,) In <p(x,) Ax, y p(x,) tp(x_t) Ax,

exp —--< —-.

y P(x,) Ax,    y p(xt) A x_t

Wszystkie występujące tu sumy mają postać sum całkowych i przyAx,-*0 dążą do odpowiednich całek. W ten sposób w granicy otrzymujemy nierówność całkową

J p(x) In <p(x) dx

exp --

J‘ p( x) dx

/ P(x) ’p(x) dx

< -2—--

f p(x) dx

analogiczną z (12).

W szczególności dla p(x) = 1 mamy

exp

dx .

Wyrażenie stojące po prawej stronie nazywa się średnią arytmetyczną wartości funkcji <p(x) w przedziale <«, by, a wyrażenie po lewej stronie-średnią geometryczną tej funkcji.

2) Wyprowadzimy teraz nierówności całkowe analogiczne do nierówności Cauchy’ego-Hó!dera oraz nierówności Minkowskiego [133, (5) i (7)]:

<D>    ‘ir

on    < (E-tT+{£*&'"•

gdzie k, k’> 1

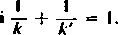
Niech dane będą w przedziale <a, b) dwie funkcje dodatnie (p(x) i yi(x); rozbijmy, jak wyżej, ten odcinek za pomocą punktów x, i podstawmy w (13)

Oi = rp(Xi)Ax'.^lk,    b, = tf'(Xi) Ax]^tk',

a w (14)

Otrzymujemy

a, - <p(x,) Ax)'^k,    b, = ■/’(*,) Ax\^lk.

y (Xi) ip (x_t) AX, < {y [ęj(.v,)]^kżlAr,}'^A{y [yi (.r,)]¹^*,}¹'*'

{y [<?(xi)+ił>(x_l)]^kAx_lyⁱ¹' <{y [yor^iM-ry ^,i+{y    '

Przechodząc do granicy przy Ax,-*0, otrzymujemy ostatecznie

(13*)

/ <pxpdx J (p^kdxy^k^j \p^k'dxy^lk'

oraz (14*)