34664

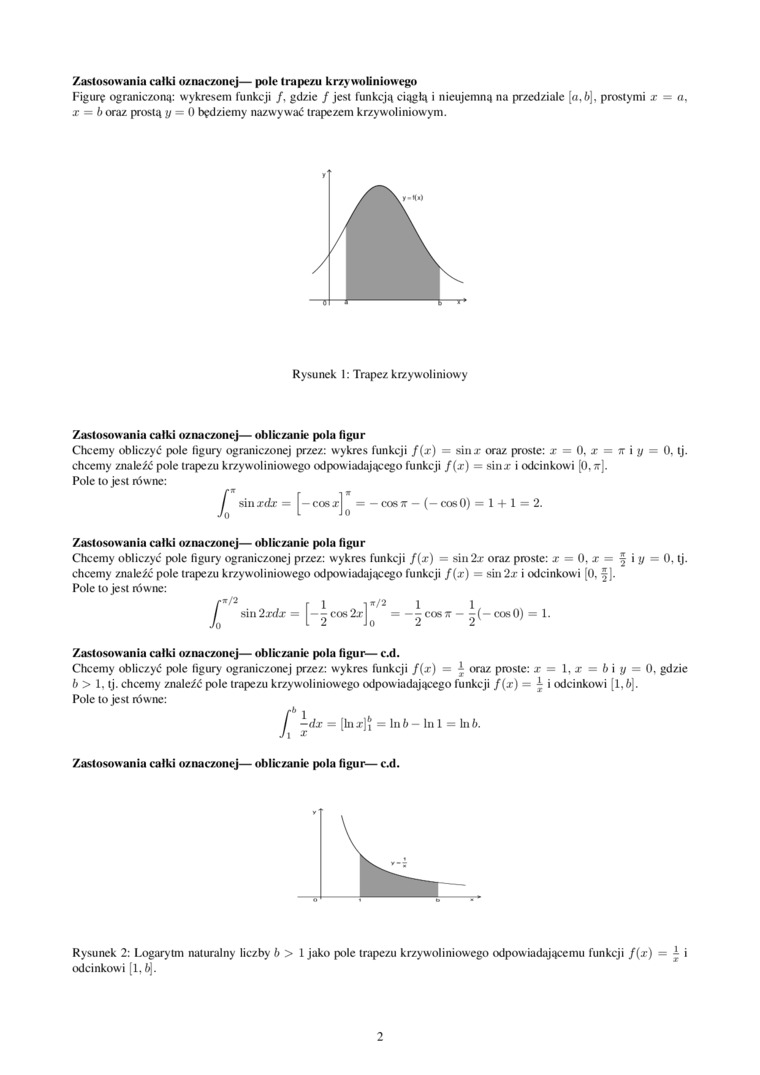
Zastosowania całki oznaczonej— pole trapezu krzy woliniowego

Figurę ograniczony: wykresem funkcji /. gdzie / jest funkcją ciągłą i nieujemną na przedziale [a, 6], prostymi x = a. x = 6 oraz prostą y = 0 będziemy nazwy wać trapezem krzywoliniowym.

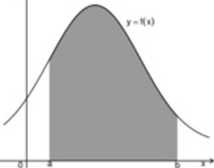
Rysunek I: Trapez krzywoliniowy

Zastosowania całki oznaczonej— obliczanie pola figur

Chcemy obliczyć pole figury ograniczonej przez: wykres funkcji f(x) = sinx oraz proste: x = 0, x = ir i y = 0, tj. chcemy znaleźć pole trapezu krzywoliniowego odpowiadającego funkcji f{x) = sinx i odcinkowi [0. *].

Pole to jest równe:

J sinxdx = cosxj_o = — cosx - (— cosO) = 1 + 1 = 2.

Zastosowania całki oznaczonej— obliczanie pola figur

Chcemy obliczyć pole figury ograniczonej przez: wykres funkcji f(x) — sin2x oraz proste: x = 0, x = % i y - 0, tj. chcemy znaleźć pole trapezu krzywoliniowego odpowiadającego funkcji f(x) = sin 2x i odcinkowi [0, ^].

Pole to jest równe:

z*/J

/ ^S Jo

sin 2xdx = - - cos 2x 2 Jo

*/² 1 1

= --cos* - -(-cosO) = 1.

Zastosowania całki oznaczonej— obliczanie pola figur— c.d.

Chcemy obliczyć pole figury ograniczonej przez: wykres funkcji f(x) = £ oraz proste: x = 1, x = 6 i y = 0, gdzie 6 > 1. tj. chcemy znaleźć pole trapezu krzywoliniowego odpowiadającego funkcji f(x) = j i odcinkowi [1,6].

Pole to jest równe:

[ —dx = [lnx]| = ln 6— In 1 = In 6.

J i x

Zastosowania całki oznaczonej— obliczanie pola figur— c.d.

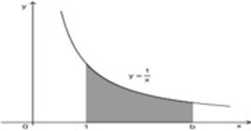
Rysunek 2: Logarytm naturalny liczby 6 > 1 jako pole trapezu krzywoliniowego odpowiadającemu funkcji /(x) = j i odcinkowi [1,6].

2