191

380 XIX. Całki oznaczone

19.47.    Obliczyć pole obszaru ograniczonego parabolą y — 2x — x² i prostą ^

19.48.    W jakim stosunku parabola y² — 2x dzieli pole kola x² +y² = 8.

19.49.    Obliczyć pole zawarte pomiędzy hiperbolą xy = 4 a prostą x+j>=5.

19.50.    Obliczyć pole wspólnej części wnętrza okręgu (x—6)²+y² = 36 i parab₀i-y² = 6x.

19.51.    Obliczyć pole ograniczone linią j = xsin4x, odcinkiem osi Ox w przedzie oraz rzędną w punkcie x=\n.

19.52.    Obliczyć pole ograniczone linią y=xe~^2x, odcinkiem osi Ox w przedziale i rzędną w punkcie x=$.

19.53.    Obliczyć pole ograniczone linią j=xcos^x, odcinkiem osi Ox w przedziale ^n^x^n i rzędnymi w punktach x=$k i x=n.

ZASTOSOWANIA GEOMETRYCZNE CAŁEK

$ 20.1. OBLICZANIE PÓL, GDY LINIA OGRANICZAJĄCA JEST OKREŚLONA W POSTACI PARAMETRYCZNEJ LUB WE WSPÓŁRZĘDNYCH BIEGUNOWYCH

Jeżeli dana krzywa jest określona równaniami w postaci parametrycznej x=g(/), y=h(t), gdzie funkcje g(t) i h(t) są ciągłe w przedziale    a przy tym funkcja g(t)

jest rosnąca (rys. 20.la) i ma w tym przedziale pochodną ciągłą, to pole obszaru (rys. 20.1)

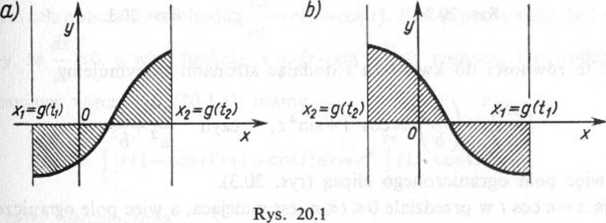
ograniczonego lukiem danej krzywej, odcinkiem osi Ox oraz prostymi x=x_lt x=x₂, gdzie x₁=g(t_l), x₂=g(r₂), wyraża się wzorem

⁽²⁰'U)    P= J \y\dx= J \h(t)\g'(t)dt.

xi    ri

Jeżeli przy tych samych założeniach funkcja g(t) jest malejąca (rys. 20.Ib) w przedziale to pole obszaru wyraża się wzorem

(20-1.2)    P = J |y|dx= - J \h(t)\g'(t)dt.

Xi    t j

Jeżeli krzywa dana jest we współrzędnych biegunowych r =/(#), gdzie /(0) jest funkcją ⁿⁱeujemną ciągłą w przedziale a $ 0 </?, a przy tym 0 <fi — a < 2tt, to pole obszaru (rys. 20.2) graniczonego łukiem krzywej r=f{6) oraz promieniami wodzącymi o amplitudach a i fi ^raża się wzorem

⁽20-i.3)    P=^l2$>-²de=łS(_m)²de.

«    a